2022.01.21

☆今すぐ使える☆１%の努力でできる算数の授業スキル「用途に応じて並べ方を変える」（No.6）

前回に引き続き、今回紹介する算数の授業スキルは、算数の授業を得意とする先生の９割が実践しています。
しかも、とっても簡単で、今すぐ使えて、たった１%の努力でできる算数のスキルなのです。今回はそのスキルの第6弾「用途に応じて並べ方を変える」について紹介します。

東京学芸大学附属大泉小学校　教諭　神保　勇児

変化を見せたいときは横に並べる

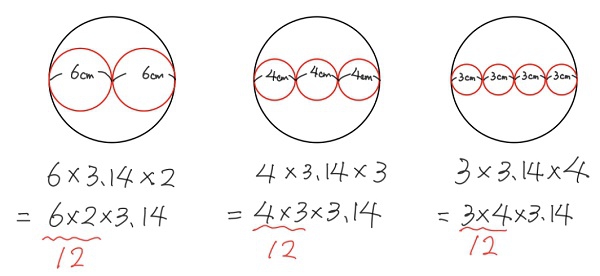
図１　円周の長さは同じ？（左右に並べる）

図１を見てみましょう。これは、第５学年「円と円周」の学習です。
ここでは、円の円周の長さを求める問題を扱います。例えば、「外側の縁の円周の長さと内側の円の円周の長さの合計は同じかどうか」という問題があります。この問題では、最初に内側の円の数が２個の場合を考えます。その後、３個、４個と円の数を変えたとき、外側の円の円周の長さと内側の円周の長さの合計はどうなるかと考えを広げていきます。

このとき、図を左右に並べると、内側の円の数は右にいくにつれて多くなり、左にいくにつれて少なくなります。左右に並べるのには理由があります。左右に並べることで、数の変化を表や数直線図で表すときに都合がよくなるからです。

式を比較したいときは上下に並べる

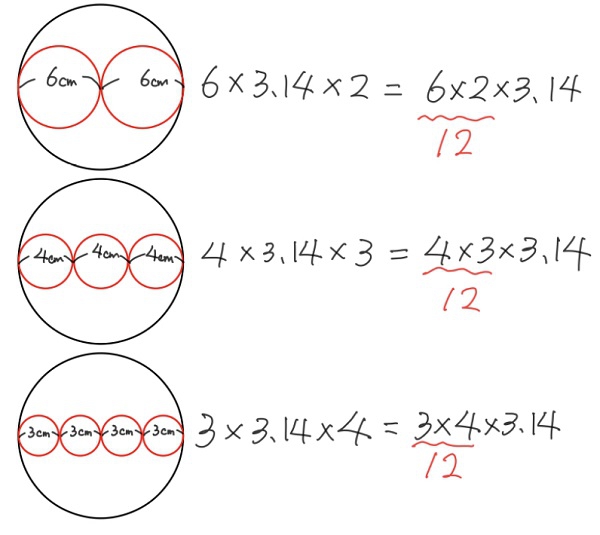
図２　円周の長さは同じ？（上下に並べる）

次に図２を見てみましょう。先ほどと単元や問題は同じです。違うのは、図と式が上下に並んでいることです。
この並べ方で、円の数の変化を見ようとすることもできます。しかし、人によっては、円の数の変化が見づらいために、表や数直線図に表そうとする発想が起こりにくくなってしまいます。それは、図２は上から下に円の数が多くなっているのに対して、表や数直線に表す時は左から右に円の数が多くなるように表すからです。ちょっとした違いが、子どもの学習活動に影響を与えます。ちょっと見づらいと感じることで、変化を見ようとする意識が低くなることにつながるからです。

では、このような図の表し方はどのようなときに都合がよいのでしょうか？それは、式を見比べるときです。式を上下に並べることで、式のどの部分が同じか、違うかがわかりやすくなります。先ほどの左右で並べた図の式と見比べてみてください。上下に並べた時の方が「12」になる部分と「3.14」が見やすくなっています。

また、式を上下に並べることによって、新たな3つの考えが出てきやすくなります。

◆「6×2」「4×3」「3×4」は内側の円の直径の合計が12になること

◆内側の円の直径の合計 12は外側の円の直径と同じであること

◆計算しなくても、外側の円の円周の長さと内側の円の円周の長さは同じなのはわかること

私が授業をしたときには、子どもが「直径（内側の円の直径の合計）×3.14」という公式を作りました。

今回のスキル「用途に応じて並べ方を変える」はいかがだったでしょうか。ご自身の学年の単元でぜひ活用してみてください。
今回のスキルにつながる内容は、授業スキルアップ研究会や『学び合いコーディネートスキル60』（明治図書）で扱っていますので、ぜひ参考にしてみてください。

※画像は筆者作成

参考資料

『学び合いコーディネートスキル60』（明治図書）

神保　勇児（じんぼ　ゆうじ）

東京学芸大学附属大泉小学校　教諭

2020年度はコロナウィルスでの休校期間でオンライン授業を多く行うことがありました。その時に得た、オンラインでも使える問題の見つけ方、子供の自力解決の見取り方、つぶやきの拾い方、発表検討のさせ方など紹介していきます。
「jimbochanのブログ」https://jimbochan.hatenablog.com/