子供の問いを引き出す(21) 数学史からの教材(かけ算の筆算):3年「格子かけ算」 スクールプレゼンターで問いを引き出す算数授業づくり(第27回)

算数用アプリ「スクールプレゼンターEX(以下スクプレ)」を使って子供の問いを引き出す算数授業の実践紹介。今回は「カジョリ初等数学史」からの教材です。
「3桁でもできるかな?」を引き出す
この本と出合ったのは15年前の月例の読書会です。この本が課題図書でした。この読書会の進め方は、1行ずつ参加者で交代して読み、そこで気になった部分を自由に話し合います。この読書会のおかげで、一人だと理解できない部分も理解することができたり、関連した話題について知ったり、今回の教材のような小学校の教科書では扱われていない面白い教材にも出合ったりすることができました。
もし、算数を勉強したいと思っている仲間で勉強会をするなら、その入口は読書会がお薦めだと思います。まずは、学習指導要領算数編や今使用している算数の教科書から始めるといいでしょう。今なら、Zoomなどのミーティングアプリを使って遠方の方とも一緒に勉強できます。1回の読書会で進む頁は少ないですが、一人で読むより、深い学びが生まれます。
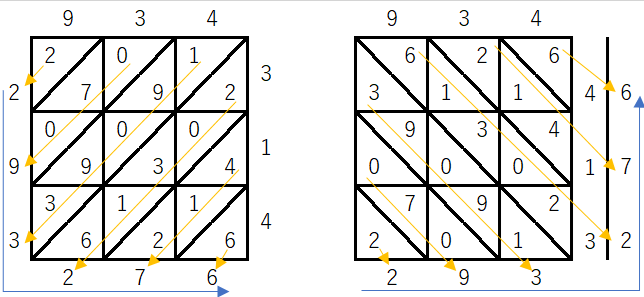
「トレヴィソ算術(1478年)」の「934×314=293276」のかけ算の図
教材の話に戻ります。
この本には、「トレヴィソ算術(1478年)」の「934×314=293276」のかけ算の図が紹介されています。この方法を「格子かけ算」と呼ぶそうです。
私はこの「格子かけ算」を知り、まず、自分で適当な数を考えて筆算をしてみました。計算しているうちに「答えが合うのはなぜだろう?」「繰り上がりの処理が難しいかも…」「ネイピアの骨と似ているな…」と次々に問いが湧いてきました。そして、これを子供たちにもやらせてみたら、同じように問いが次々に湧いてくるかもしれないと思いました。
しかし、教材化する際に、気になったのは部分積をどこまで扱うかです。普段のかけ算の筆算で部分積について触れると一気に難しさのレベルが上がります。さらに、「格子かけ算」は斜めに見て和を出すのでさらに難しくなります。今回は対象学年が3年生であることから、もっと計算の仕方に慣れてから扱うのが適切ではないかと思いました。
以上のことから、下記の点に配慮して授業に臨むことにしました。
- 初めに提示する「格子かけ算」は、2桁×2桁で、繰り上がりのない簡単なものにする。
- 繰り上がりが出た場合は、その処理の仕方を丁寧に指導する。
- 子供たちから「3桁でもできるかも…」という問いが生まれてから、3桁×2桁を扱う。
- 部分積については、本時では無理に扱わず、計算の範囲を広げることに重点を置いて指導する。
授業の様子
まず、「イタリアのひっ算」と黒板に書き、
「この前、本を読んでいたら、昔のイタリアのかけ算の筆算の仕方を知りました。みんなに教えたいくらいびっくりしたんです。どんなやり方だと思いますか?」と話して、黒板横の電子黒板に注目させました。
スクプレで作ったスライドを、子供たちの反応を見ながら少しずつ進めていきました。
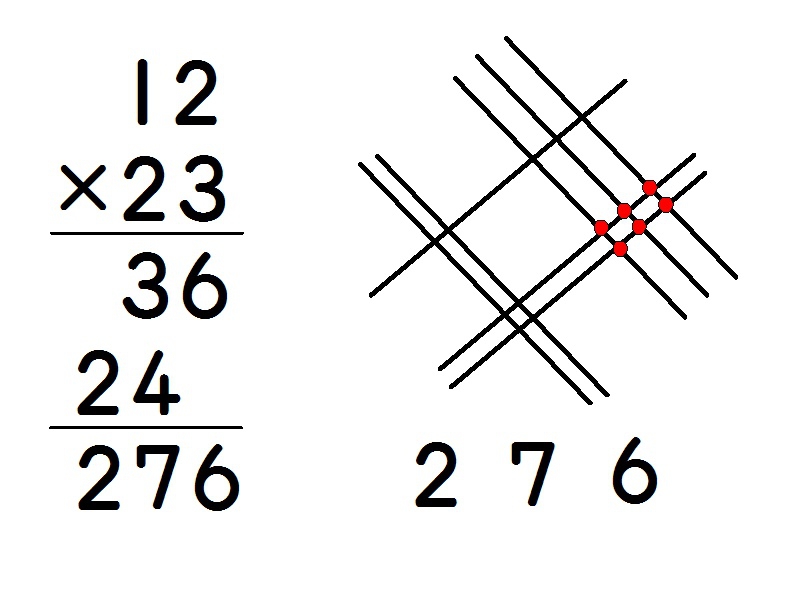
「『12×23』のやり方は知っているよ。」
「え?『田』の漢字が出てきた!」
「斜めの線?どうして?」
「02…?分かった!『1×2』の答えだ。」
「2・7・6…、276。あ!答えが同じになった。どうして?」
子供たちから格子かけ算のやり方や問いに関するつぶやきが聞こえてきました。
このようにスライドを見せて気付きを引き出す時のコツは、できるだけ画面に集中させることです。画面をシンプルにし、大きな画面に映し、音声の説明をできるだけ少なくします。不思議なもので、教師の説明がない方が画面をしっかり見るものです。
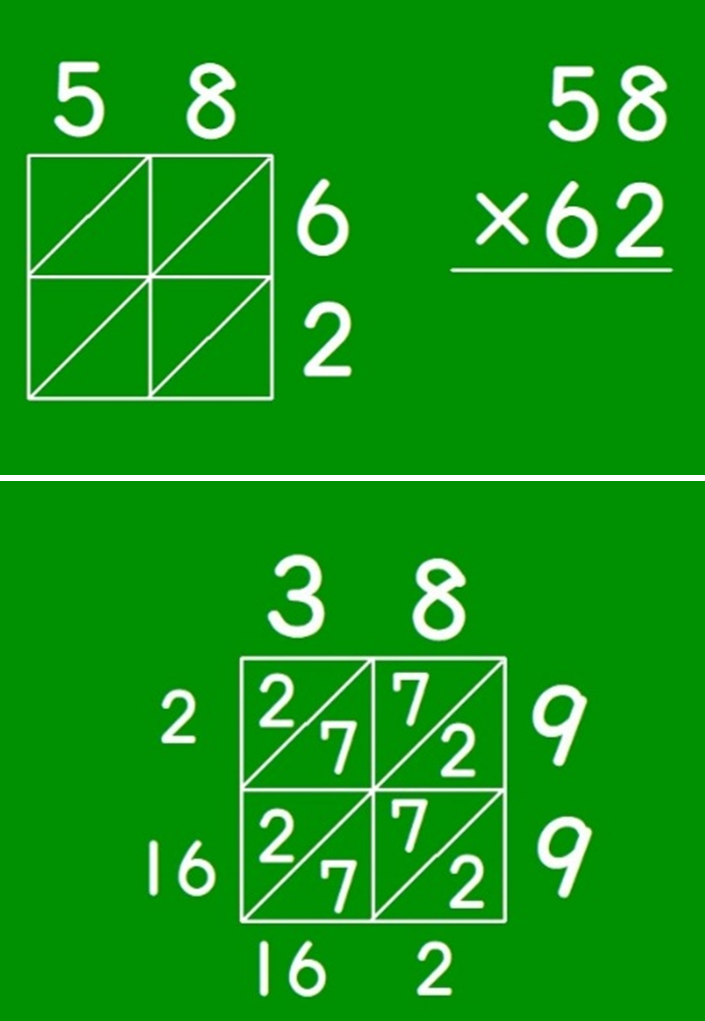
Aさんがノートに何か計算している様子が見えました。近づいてみると、「58×62」を計算しています。
「Aさんってすごいなあ!自分から進んで違う数で試しているよ。」と大きな声で褒め、Aさんが試している「58×62」のかけ算の筆算を黒板に書きました。みんなも計算に取り組み始めました。
「おお、答えが合ってる!」
「イタリアの方が簡単!」
と喜ぶ声が次々に上がりました。
その中に、「先生、私も別の数でもやってみた!」というBさんの声が聞こえました。Bさんの式を見ると、「38×99」でした。
この「99」は、子供に数を考えさせると、必ず出て来る数値です。最初にAさんが言わなかったのが不思議なくらいです。もちろん、計算の途中で、繰り上がりがあります。
あえて、繰り上がりの処理をしないままの格子かけ算を見せて、次のような発問をしました。
「イタリアの筆算の答えは、『216162』になるんだね。」
すると、子供たちから次のような声が上がりました。
「日本の筆算と比べると、答えの一の位と十の位が同じだから、おしい。」
「『16』の『1』は繰り上げるといいと思う。」
「繰り上げて計算してみたら、『3762』になって答えが同じになった。」
間違ったものを提示したことで、子供自ら繰り上がりについて適切の処理する考えを引き出すことができました。もっと深い理解をさせるには、部分積で出てきた「16」の意味や繰り上げていい理由ついて考えさせたい場面です。しかし、今回は「計算の範囲の拡張」にねらいを定めたので、ぐっと我慢しました。
次に「87×62」を計算してみました。この計算している途中で、ふとCさんがこんなことを言いました。
「だったら、3桁でもできるかも…」
黒板にこの言葉を書き留め、「87×62」が終わったら、みんなも「だったら」で考えるように準備をしました…。

※教材の作り方~頁をコピーしてスライドを作る~
-
手順1~2
-
手順2~3
-
手順4~5
今回の教材は、PowerPointやGoogleスライドで作ったような、紙芝居形式の教材です。
この教材のような画面の内容が少しずつ付け足されるタイプのスライドは、PowerPointだと「選択したスライドの複製」、Googleスライドだと「スライドのコピーの作成」を使うと、簡単に作成できます。
しかし、スクプレにはこのような機能はありません。
そこで、第24回で紹介した「すべて選ぶ(Ctrl+A)」と「貼り付けする(Ctrl+V)」を使います。これらのWindowsのショートカットキーを活用することで、スクプレでも紙芝居形式の教材が簡単に作成できるようになります。
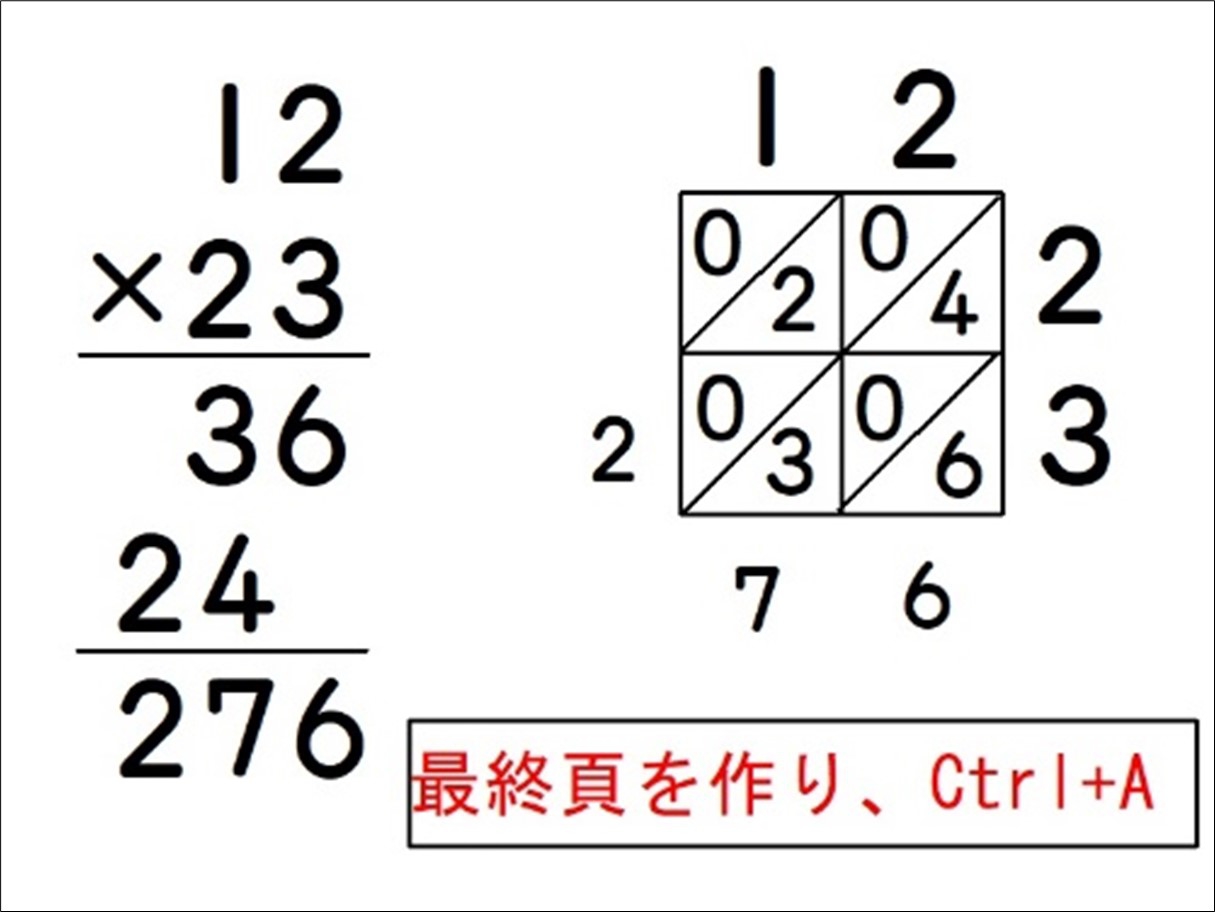
また、短時間で作るコツとして、最終頁から作ることを勧めます。
最終頁をコピーして一部分を削り、その頁をコピーして一部分を削り…を繰り返すと、びっくりするくらい速くできます。今回の教材だと、下記のような手順になります。
- まず、最終頁を作る。
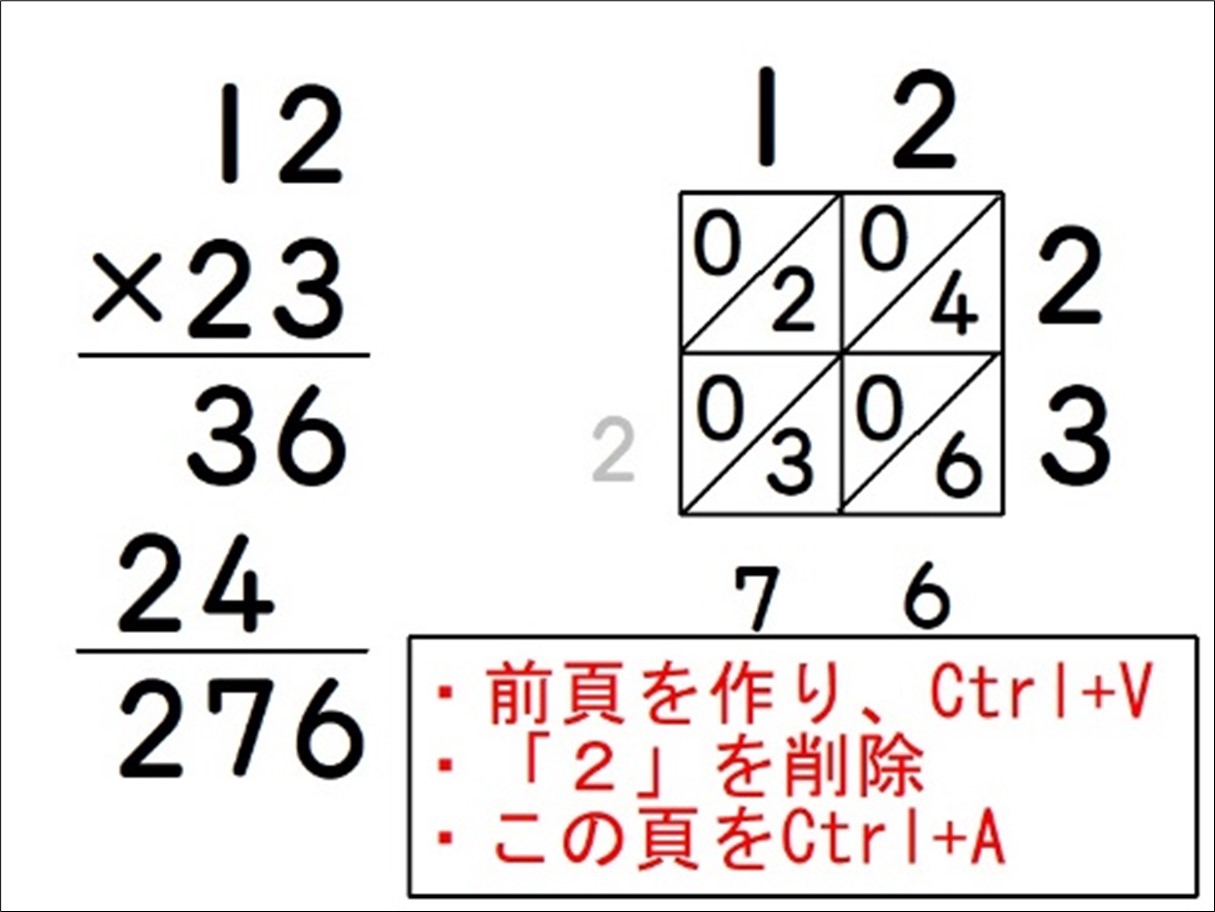
- その頁を「すべて選ぶ(Ctrl+A)」でコピーし、前の頁を新しく作り、「貼り付け(Ctrl+V)」する。
- 「2」を削除する。
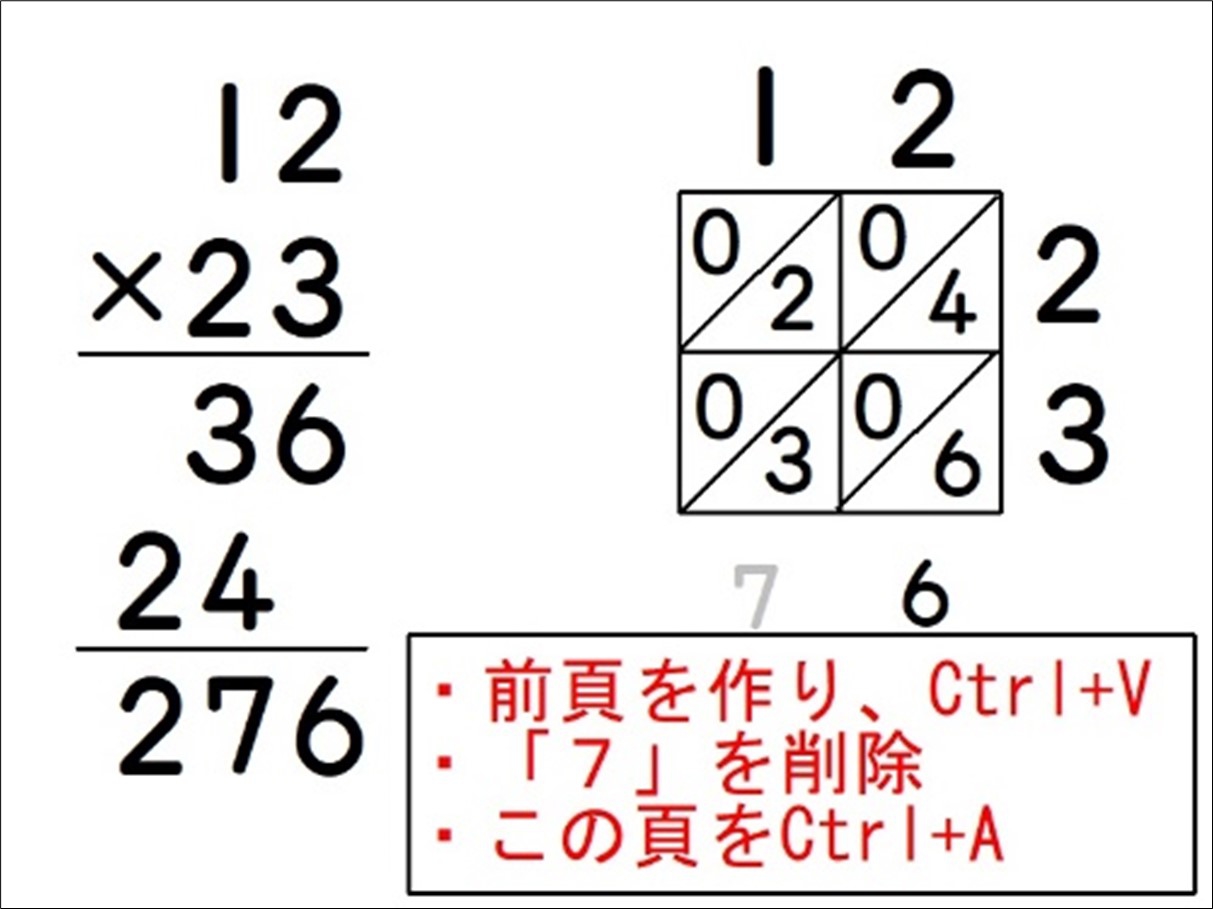
- その頁を「すべて選ぶ(Ctrl+A)」でコピーし、前の頁を新しく作り、「貼り付け(Ctrl+V)」する。
- 「7」を削除する。
※この後も「Ctrl+A→前の頁を新しく作る→Ctrl+V→一部を削除」を繰り返す。
関連するお勧め教材(「かけ算の筆算」の教材)
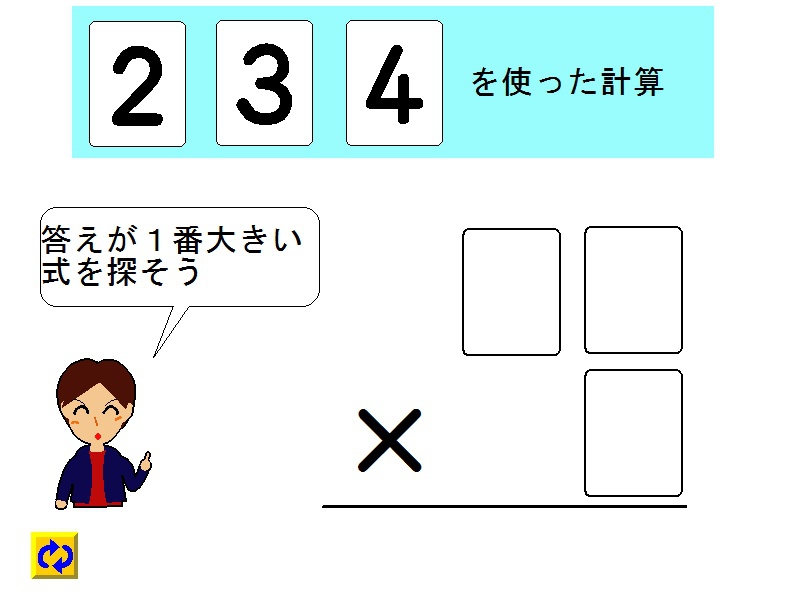
- 小3算数 2桁×1桁(数字カード)
かけ算の筆算の教材です。数字カードを使って一番大きい積の式を考えさせます。試行錯誤で式を出せますが、なぜそうなるのか論理的に説明させることもできます。数字カードに吸着の設定してあるので、気持ちよく使えます。2頁目には、発展問題が作れるように、1~9までの数字カードを用意しました。 - 小3算数 覆面算
かけ算の筆算の覆面算です。Dが繰り上がらないことからA=1となるように、筋道を立てて考えるとすべての数が分かります。カードは少しずつ見せたり、削除したりして使います。 - 小3算数 虫食い算(かけ算の筆算2)
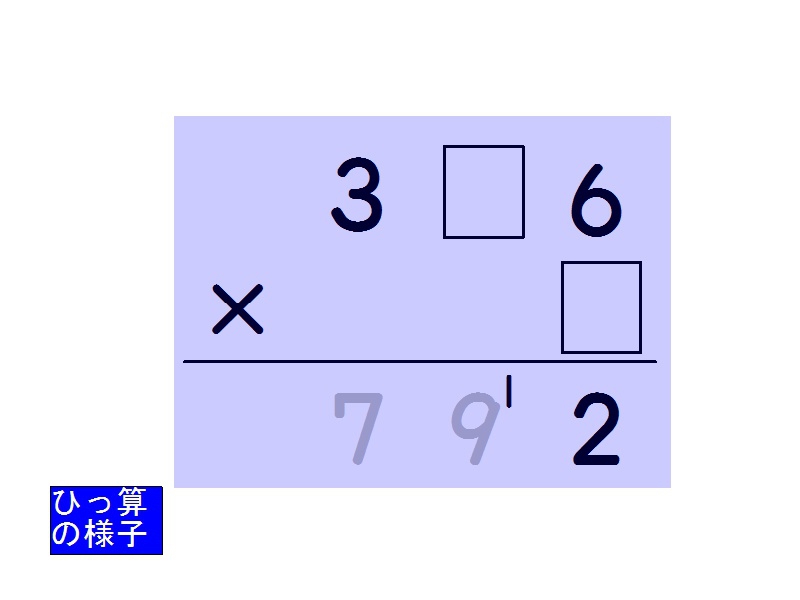
かけ算の筆算の「虫食い算」の教材です。苦手な子のために、虫食い算のまま立ててかけて引いて下ろすという筆算の過程を見せられるようにし、数字同士の関係に気付くようにしました。「ひっ算の様子」をクリックすると紙芝居のように提示できます。繰り上がりが見えるようにしました。 - 小3算数 23×12の筆算
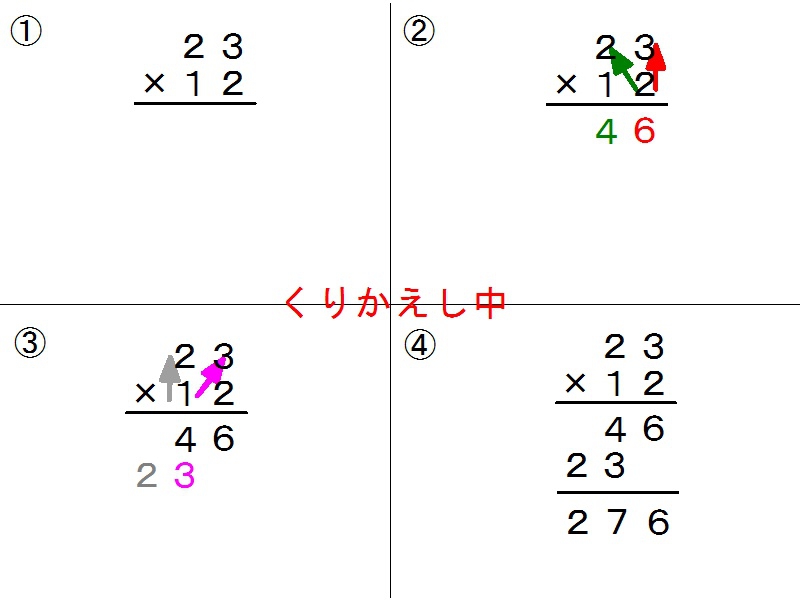
23×12の筆算の手順を図解した教材です。筆算の順番が分かるよう4コマ漫画の手法を取り入れています。自動に繰り返すこともできるので、そのまま提示して机間指導することもできます。 - 小3算数 21×13のブロック図(振り返り用)
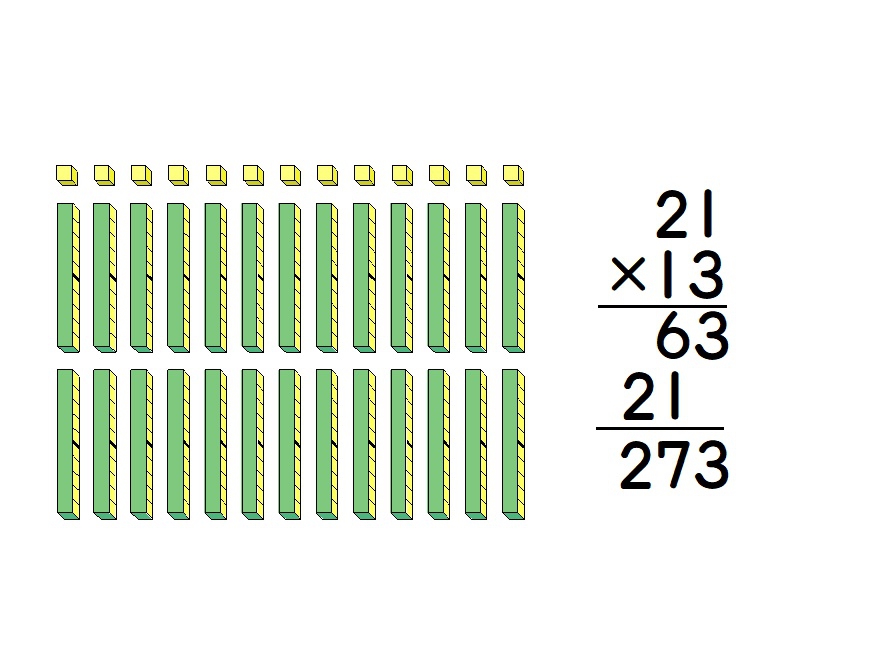
2ケタ×2ケタの筆算の教材です。振り返りの場面ではかけ算の部分積がブロック図のどの部分なのか描き込むことができます。また、問題提示の場面では、21×3の部分から21×13へ変化させることができます。 - 小3算数 速算のカード
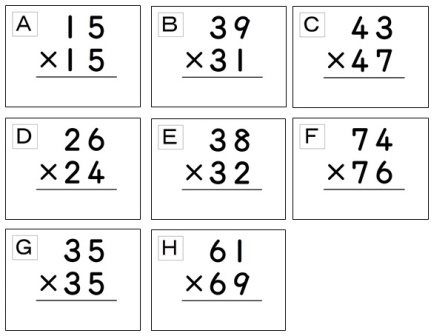
2桁×2桁の筆算の教材です。8枚のカードを隠し、子供に選ばせて、先生と子供たちで計算競争します。先生がいつも勝つことから、「何かひみつであるかも…」という気持ちを 引き出すことかできます。ひみつを見つけたら、自分で式を作る活動に発展させます。 - 小3算数 線を引くだけの筆算
かけ算の筆算の理解を深めることができるトピック教材です。 インドなどで行われている線を引くだけでできるかけ算の筆算と既習の筆算が比べられるようにしました。「どうして答えが合うのだろう?」という問いを引き出し、2つのやり方が部分積に共通部分があることに着目させていきます。 - 小5算数 小数のかけ算の筆算(数カードを使って)
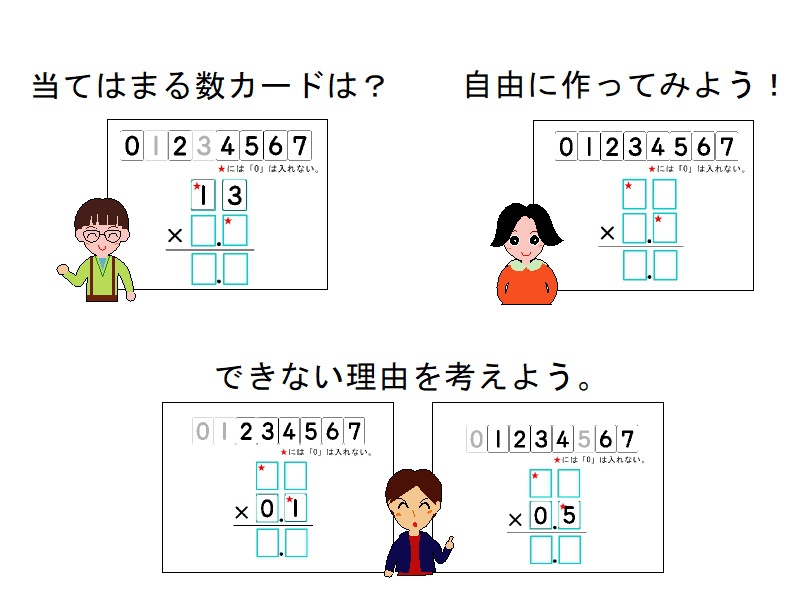
小数のかけ算の筆算の教材です。0~7までの数カードを1枚ずつ使って、成り立つ式を考えます。「かけられる数を指定した場合」「成り立たない場合」「自由に作る場合」の3パターンを用意しています。このまま印刷してワークシートとしても使えます。
こちらも是非ダウンロードして使ってみてください。次回は、4年「外国のわり算の筆算」を取り上げます。お楽しみに!
種市 芳丈(たねいち よしたけ)
階上町立道仏⼩学校 教頭
ICTを活用した算数授業に取り組んでいます。特に、「スクールプレゼンター」は10年以上使っていて、お気に入りのアプリの1つです。自分の作った教材が下記のサイトに約650ファイルほどあります。
スクールプレゼンター教材共有サイト「スクプレ道場」(※2025.3にクローズしました。)
関連記事
- 番外編「ICTを活用した図形パズル教材~子供の困ったに寄り添う~」
- 子供の問いを引き出す(27) きまり発見を楽しむ:2年「引き算」
- 子供の問いを引き出す(26) 対称の中心を探す活動:6年「対称な図形」
- 番外編「ICTを活用した乗法九九の指導」
- 子供の問いを引き出す(25) 手ごたえのある問題を:6年「分数の計算」
- 子供の問いを引き出す(24) 式と図を関連付ける:5年「体積」
- 子供の問いを引き出す(23) 夢中になる計算:4年「式と計算」
- 子供の問いを引き出す(22) 数学史からの教材:4年「いろいろな国のわり算の筆算」
- 番外編「『4コマ提示』を使った算数授業」
- 子供の問いを引き出す⑳ 「緑表紙(尋常小学算術)」の教材:5年「杉成算」
- 子供の問いを引き出す⑲ 「式の表現と読み」の教材:3年「点字ブロックのブロックはいくつ」
- 子供の問いを引き出す⑱ 動きのある教材4:2年「三角形と四角形」
- 子供の問いを引き出す⑰ 動きのある教材4:5年「図形の面積」
- ⼦供の問いを引き出す⑯ 少しずつ見せる提示:3年「1けたをかけるかけ算」
- 番外編「全国学力・学習状況調査の算数の問題のスクプレ化」
- 子供の問いを引き出す⑮ 動きのある教材3:5年「速さ」
- 子供の問いを引き出す⑭ 数字カード:6年「分数のかけ算」
- 子供の問いを引き出す⑬ 算数手品2:4年「1けたでわるわり算」
- ⼦供の問いを引き出す⑫ スポットライト提示2︓2年「かけ算(九九表)」
- ⼦供の問いを引き出す⑪ 動きのある教材2︓3年「表とグラフ」
- 番外編 GeoGebraを活用した算数授業:3年「円と球」
- 子供の問いを引き出す⑩ 算数手品:4年「変わり方」
- 子供の問いを引き出す⑨ 困っている場面に注目させる︓4年「九九の範囲を超えるわり算」
- 子供の問いを引き出す⑧ 不完全なものを提示︓3年「目盛りが足りない」
- 子供の問いを引き出す⑦ 図形の動的提示:3年「どんな三角形が見えたかな?」
- 子供の問いを引き出す⑥ スポットライト提示︓4年「正方形は何枚?」
- 番外編 Jamboardのワークシートの作り方② 動かせるワークシート
- 番外編 Jamboardのワークシートの作り方①
- 子供の問いを引き出す⑤ くじ引き:3年「三角形」
- 子供の問いを引き出す④ 筋道を立てて考える教材:5年「長方形に分けると」
- 子供の問いを引き出す➂ 動きのある教材:3年「エレベーター(植木算)」
- 子供の問いを引き出す➁ 意図的な数値を設定:4年「分数」
- 子供の問いを引き出す① 違い探し:4年「位置の表し方」
- <新連載>スクールプレゼンターで問いを引き出す算数授業づくり[第1回]
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



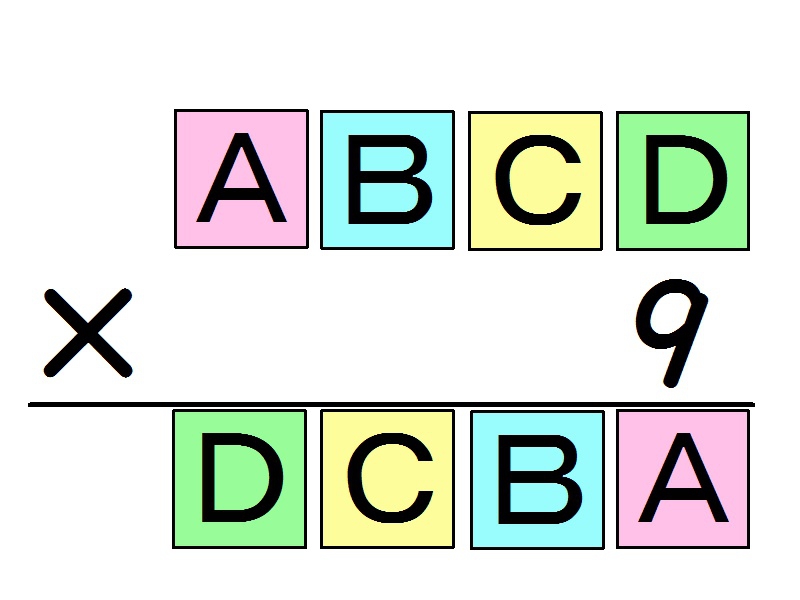
 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
