番外編「『4コマ提示』を使った算数授業」 スクールプレゼンターで問いを引き出す算数授業づくり(第26回)
今回は番外編として、スクールプレゼンター(以下スクプレ)を使って、作図の手順などを1画面に4分割して示す「4コマ提示」教材を紹介します。
子供にも先生にもやさしい「4コマ提示」
作図指導や折り紙を使った構成活動、比べる活動、問題提示などに効果的
「4コマ提示」を思いついたのは、作図指導の時です。
「先生と一緒に作図するよ。」と指示を出し、実物投影機を使って一緒に大きな画面に映して指導していました。すると、「先生、なんか違う線になっちゃう…」という声が上がったので、その子の近くに行って個別指導をすると、今度は別の子から、「終わったけど、次はどうすればいいですか?」と声が上がり、その子の近くに行って指示しました。すると、また別の子が…のようなことの繰り返しでした。
この方法だと私だけ忙しく動くわりに、子供たちの待っている時間が増えます。この方法でうまく進めるには数人の先生が必要だと思いました。でも、学級担任は基本的に一人で指導するので、何か別のアイディアが必要です。
そこで、スクプレを使って、手順を1画面に4分割して示す方法(「4コマ提示」と名付けました)を思いつきました。手順を最初に示し、つまずきそうな箇所はアニメで作ります。作図の手順を4つにまとめたので、作図の全体の流れが見え、子供たちが自分で次にすることを考えたり、ちょっと遅れた子も自力で追いついたりすることができるのもいいと思いました。
実際、授業で取り組んでみると、子供たちが作図している間は、机間指導に重点を置いて教えることができました。これなら一人で作図指導しても、子供たちの待ち時間もかなり少なくなりました。また、作図の学習は子供たちが受け身になりがちですが、子供自身で考える場面も増えました。
だったら、作図指導以外で使えないか考えました。
次に思いついたのは「折り紙」です。折り紙を使った構成活動も、待ち時間が多く、子供たちが受け身になりがちだったからです。つまずきの多い折る場面はアニメを使って提示したことで間違いがかなり減り、「できた!」と喜ぶ姿を多く見られるようになりました。
さらに思いついたのは、比べる活動がある学習での活用です。作図や折り紙は、前に示した図と比べて、次を考えます。この様子は、多様な考え方をねらう学習と少し似ています。また、振り返りの場面では、今までの考えを見比べて共通点を考えるので、「4コマ提示」は適していると思いました。
最近は、問題提示での活用に取り組んでいます。算数が嫌いになる要素の一つに算数独特の言い回しや表現があり、テキストで表示されると問題把握ができない子が見られます。そんな子の中には、隣で読んであげたりその子が分かる表現に置き換えてあげたりすると、すらすらと解けてしまうことも珍しくありません。これを非テキストである「4コマ提示」でやろうと考えました。実際、授業をしてみると「何だかマンガで問題を出されているみたいで楽しい」と子供たちに好評でした。
上記のような試行錯誤で取り組んできた「4コマ提示」ですが、メリットをまとめると、下記の5つ挙げられます。下記の「お勧めの『4コマ提示』教材」と合わせてご覧ください。
- 作図指導で活用すると、分かり易くなり、見通しももてる。
- 折り紙の学習でも、分かり易くなり、見通しももてる。
- 4コマ目を隠すことで、「たぶんこうなると思う」という問いを引き出すことができる。
- 比べる活動により多様な考えを引き出され、振り返る場面では共通点を見つけやすくなる。
- 問題提示に使うと、文章を読むのが苦手な子も理解でき、問題把握が容易になる。
お勧めの「4コマ提示」教材
①小4算数 平行な直線(メリット1)
平行な直線4コマ
平行な直線の作図の教材です。つまずきが見られる三角定規の動かし方を「アニメ」を使って作りました。また、作図全体の流れが分かるので見通しをもてたり、遅れた子も自力で追いついたりすることができます。
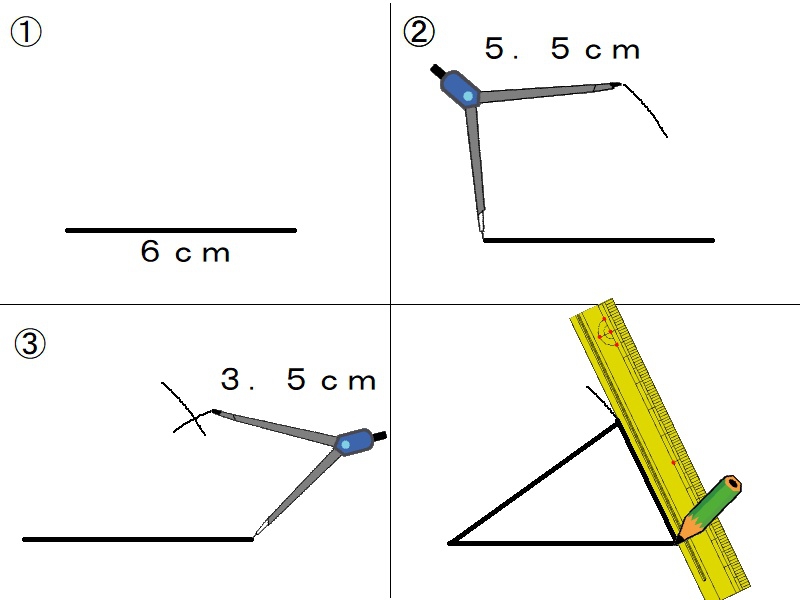
②小4算数 角度を決めて三角形をかく(メリット1)
角度を決めて三角形
作図の教材です。両端の角度が決まっている時の三角形の描き方を順番に提示できます。つまずきが見られる分度器の使い方や直線の引き方をアニメで作りました。自動で繰り返し再生もできるので、個別指導に重点を置いて指導できます。
③小3算数 折り紙で正三角形(メリット2)
折り紙で正三角形(4コマ)
折り紙を使った正三角形の作り方です。つまずきが見られる折る場面(②)をアニメにして分かり易くしました。折り紙を使った学習は折る経験の差が大きいため、個別指導が必要な場合が多いですが、4コマ提示により、そちらに重点を置いて指導できます。
④小3算数 折り紙で二等辺三角形(メリット2・3)
折って紙を切ったら…
折り紙を使った二等辺三角形の作り方です。この教材は折る場面が少ないため、個別指導の機会は少なくて済みます。そこで、4コマ目を隠し、図形の性質を考えように作りました。どのような三角形ができるか予想させ、その理由を考えさてから活動に取り組ませると、図形の性質の理解が深まります。
⑤小5算数 折り紙で正多角形(正六角形)(メリット2・3)
折り紙で正多角形(正六角形)
折り紙を使った正六角形の作り方です。つまずきが多く見られる分度器で測る場面と折る場面をアニメにして分かり易くしました。また、4コマ目を隠し、問いを引き出すように作りました。「辺が等しくなるのは何本あるか」「中心の角度は何度になるか」などを考えさせてから取り組ませると、図形の性質を意識した学習になります。
⑥小5算数 12cm3 作り(メリット4)
12cm3作り
体積の教材です。12cm3の体積になる形を、画面上でいろいろ作ることができます。前に作った形と比較することができるので、「ほかにはないかな?」と多様な考えを引き出すことができます。また、具体物でも同様の活動はできますが、整理整頓が苦手な子が多い場合には、こちらの方が学習に集中できます。
⑦小5算数 平行四辺形の面積(メリット4)
平行四辺形の面積4コマ
平行四辺形の面積の教材です。平行四辺形を長方形に等積変形する方法を、画面上でいろいろ作ることができます。前に作った形と比較することができるので、「他の方法はないかな?」と多様な考えを引き出すことができます。また、振り返りの場面では、共通していることを考えさせることで、統合的な見方も引き出すことができます。
⑧小3算数 9のあるたし算(メリット3・5)
9のあるたし算回文(4コマ)
3桁のたし算の教材です。文では説明が長くなるパリンドローム(回文数)のやり方を4コマ提示にしました。4コマ目をあえて空白にして、「どんな計算をすると思う?」と投げかけ、49以上は自分の好きな数で確かめる場が生まれるようにし、追究する姿を引き出すようにしました。
⑨小4算数 円を使ったひし形の作図(メリット5)
円を使ったひし形の作図
円を使ったひし形の作図について、どうしてひし形になるのか理由を説明する活用問題です。文では説明が長くなる円を使ったひし形の作図を4コマ提示にし、分かりやすくしました。自動繰り返し再生もできるので、じっくり見ながら考えられるようにしています。
次回は、3年「格子かけ算」を取り上げます。お楽しみに!
種市 芳丈(たねいち よしたけ)
階上町立道仏⼩学校 教頭
ICTを活用した算数授業に取り組んでいます。特に、「スクールプレゼンター」は10年以上使っていて、お気に入りのアプリの1つです。自分の作った教材が下記のサイトに約650ファイルほどあります。
スクールプレゼンター教材共有サイト「スクプレ道場」(※2025.3にクローズしました。)
関連記事
- 番外編「ICTを活用した図形パズル教材~子供の困ったに寄り添う~」
- 子供の問いを引き出す(27) きまり発見を楽しむ:2年「引き算」
- 子供の問いを引き出す(26) 対称の中心を探す活動:6年「対称な図形」
- 番外編「ICTを活用した乗法九九の指導」
- 子供の問いを引き出す(25) 手ごたえのある問題を:6年「分数の計算」
- 子供の問いを引き出す(24) 式と図を関連付ける:5年「体積」
- 子供の問いを引き出す(23) 夢中になる計算:4年「式と計算」
- 子供の問いを引き出す(22) 数学史からの教材:4年「いろいろな国のわり算の筆算」
- 子供の問いを引き出す(21) 数学史からの教材(かけ算の筆算):3年「格子かけ算」
- 子供の問いを引き出す⑳ 「緑表紙(尋常小学算術)」の教材:5年「杉成算」
- 子供の問いを引き出す⑲ 「式の表現と読み」の教材:3年「点字ブロックのブロックはいくつ」
- 子供の問いを引き出す⑱ 動きのある教材4:2年「三角形と四角形」
- 子供の問いを引き出す⑰ 動きのある教材4:5年「図形の面積」
- ⼦供の問いを引き出す⑯ 少しずつ見せる提示:3年「1けたをかけるかけ算」
- 番外編「全国学力・学習状況調査の算数の問題のスクプレ化」
- 子供の問いを引き出す⑮ 動きのある教材3:5年「速さ」
- 子供の問いを引き出す⑭ 数字カード:6年「分数のかけ算」
- 子供の問いを引き出す⑬ 算数手品2:4年「1けたでわるわり算」
- ⼦供の問いを引き出す⑫ スポットライト提示2︓2年「かけ算(九九表)」
- ⼦供の問いを引き出す⑪ 動きのある教材2︓3年「表とグラフ」
- 番外編 GeoGebraを活用した算数授業:3年「円と球」
- 子供の問いを引き出す⑩ 算数手品:4年「変わり方」
- 子供の問いを引き出す⑨ 困っている場面に注目させる︓4年「九九の範囲を超えるわり算」
- 子供の問いを引き出す⑧ 不完全なものを提示︓3年「目盛りが足りない」
- 子供の問いを引き出す⑦ 図形の動的提示:3年「どんな三角形が見えたかな?」
- 子供の問いを引き出す⑥ スポットライト提示︓4年「正方形は何枚?」
- 番外編 Jamboardのワークシートの作り方② 動かせるワークシート
- 番外編 Jamboardのワークシートの作り方①
- 子供の問いを引き出す⑤ くじ引き:3年「三角形」
- 子供の問いを引き出す④ 筋道を立てて考える教材:5年「長方形に分けると」
- 子供の問いを引き出す➂ 動きのある教材:3年「エレベーター(植木算)」
- 子供の問いを引き出す➁ 意図的な数値を設定:4年「分数」
- 子供の問いを引き出す① 違い探し:4年「位置の表し方」
- <新連載>スクールプレゼンターで問いを引き出す算数授業づくり[第1回]
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
