2025.06.18

なぜ算数を学ぶのか？「自分の考えを相手に理解してもらうため」（４）

算数を研究して18年間。様々なテーマで研究をしてきましたが、学校教育で算数を学ぶ意義は何なのかは、私なりの大きなテーマでした。
これまでの研究を通しての私の見解を10個に整理し、ここに実際の算数指導とともに紹介させていただきます。
第4回の今回は「自分の考えを相手に理解してもらうため」です。

東京都品川区立学校　平野　正隆

はじめに

教師は「なぜ算数を学ぶのか」という学習の意義を理解したうえで授業を組み立てていく必要があります。そうすることで「何を学ぶか」だけでなく「どのように学ぶか」も重視した授業改善をすることができます。
また、児童も学習する意義を実感しながら学び進める必要があります。点数や偏差値、順位といった他者との比較ばかり気にして、本来身に付けるべき方向性を見失っている子が少なくありません。果たして算数は、難しい問題を解いたり、テストの点数を取れたりすれば、それでいいのでしょうか。もちろん、様々な問題を解く力は重要ですが、生きてはたらく力を育むためには、その過程で身に付く力があることも忘れてはいけません。

相手に思いを伝えられるようになる

子どもたちが自分の主張を通そうとするとき、感情が先走ってうまく考えを伝えられない場面をみたことはありませんか。
自分の考えや気持ちを正確に言葉にする力は、経験によって養われます。算数の学習を通して、順序立てて情報を伝える力を高めることができます。説明が筋道立っていると、主張や意見がより説得力を持つようになり、自分の意見を通しやすくもなります。

また、自らの考えを説明をすることで、自分自身も情報を整理することができます。「言語化は思考の鏡」、説明する過程で、曖昧さに気付いたり、優先順位や因果関係を見直したりすることができます。算数の学習を通して、そういった経験を積むことができます。

算数における言語化

算数の学習では、「ＡはＢである。なぜなら、ＣがＤだからである」のように、明確な根拠をもって考え、それを筋道立てて説明したり、書き記したりします。数学的なパターンや関係を見つけるための考え方、証明の方法を学ぶことで、論理的思考力を高めることができます。

これは、相手に自らの考えを理解してもらうために重要な力となります。
例えば、「すべての長方形が拡大図・縮図の関係にあるとは限りません。なぜなら、長方形は全ての角が直角なので、対応する角の大きさは等しいですが、対応する辺の比が等しくなるとは限らないからです」というように、根拠を明確にしながら説明することで、相手に理解してもらうことができます。
日常生活の中でも、「遅刻しないように学校に来てください。なぜなら、登校時間がずれると安全面も心配ですし、朝の支度も遅れてしまうからです」など、様々な場面で筋道立てた説明は必要になってきます。
また、数値化された情報は、正確に伝わりやすく、信頼性も高くなります。例えば、「この前のテストは、みんなができなかったんだよ」よりも、「この前のテストは、みんなができなくて、平均点が50点だったんだよ」と話したほうが、「できなかったこと」が伝わりやすいです。
このように、物事を説得する場面でも、算数で身に付けた力が有効に働きます。算数を通して、コミュニケーション能力を高めることができるのです。

指導の工夫

下記の実践では、めあてを「説明しよう」とし、グループ活動や全体の場で説明する機会を設けています。全体の場でいきなり発表できるのは、よっぽど自信がある子だけです。しかし、グループの中で気付いた子が一旦説明すると、友達に理解されたという自信から挙手できるようになります。
また、自分だけでは分からなかった子も、グループ活動の中で理解し、全体の場で発表することがあります。

私の授業では、グループ内で解決に至らない場合には、他グループの説明を聞きに行ったり、助けを求めたりしても良いこととしています。その後、得た情報を自らのグループで共有することで、解決への糸口にします。

また、自力解決とグループでの学び合いの時間は分けず、各グループの学習進度に合わせてよいこととしています。
このようにして、コミュニケーションをとりながら、解決に向かわせていきます。

実践「偶数・奇数」(第５学年)

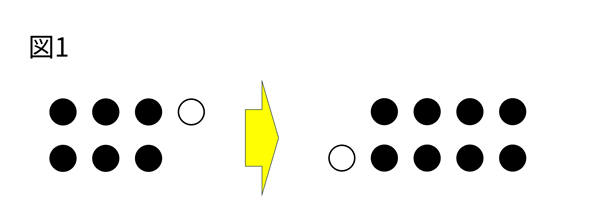
図1

教師：Aさん、好きな奇数を１つ言ってください。
児童A：13

教師：では、Bさん、好きな奇数を１つ言ってください。
児童B：9

教師：この奇数同士を足すと、どんな数になりますか。
児童：22
　　：ゾロ目だ。
　　：いつもゾロ目になるわけじゃないよ。
　　：偶数になってる。
　　：他の奇数を足してもそうなるのかな。

教師：試してみたらいいんじゃないかな。

(試す時間をとる)

児童：偶数になる。

<めあて>
奇数と奇数の和が偶数になる理由を説明しよう

教師：班で協力して考えてもいいからね。

（自力解決・学び合い・グループ活動）

教師：では、全体の場で説明できそうな人はいますか。（指名）
児童：偶数は２の倍数なので、２×ａと表せます。奇数は２の倍数に１を足した数なので、２×ａ+１と表せます。奇数同士の和は、この「１」が２つ分になるので、偶数になります。
児童：偶数を図に表すと、縦に２個ずつ切りよく⚫︎が並びます。奇数を図に表すと、⚫︎が１つはみ出ます。これを分かりやすく⚪︎とします。奇数同士の和は、図のように、この⚪︎が合わさるため、偶数になります。

児童：「偶数+偶数」や「偶数+奇数」は、どうなるんだろう。
教師：どうなるか考えて説明してみよう。

（自力解決・学び合い・グループ活動）

教師：では、全体の場で説明できそうな人はいますか。（指名）
児童：「偶数+偶数」は、２×ａ+２×ｂとなります。どちらも２の倍数なので、足しても２の倍数となります。そのため、和は偶数です。(図2)
児童：「偶数+奇数」は、２×ａ+２×ｂ+１となります。奇数の⚪︎が１つ残るので、和は奇数です。(図3)

まとめ

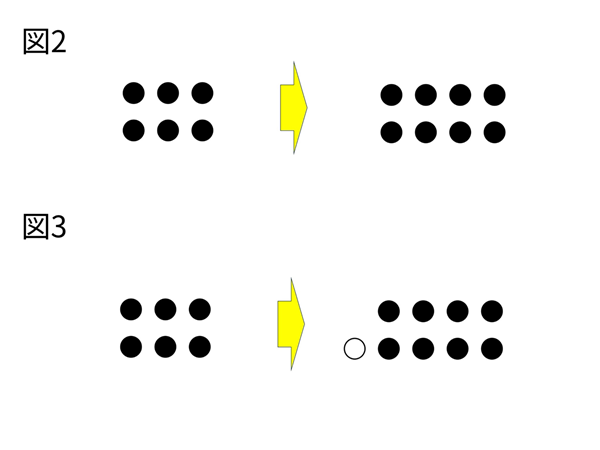
図２・図３

このように、算数は「数や図形の学び」だけではなく、「思考を整理して伝える」「人の話を理解する」という、対話を通じて共に学ぶ教科でもあるのです。
したがって、学校で算数を学ぶことで、子どもたちのコミュニケーション能力を育てることにもなり、やがて相手に自らの思いを上手に伝えられるようになっていくと信じています。