2025.09.08

なぜ算数を学ぶのか？「見通しをもって生活するため」（８）

算数を研究して18年間。様々なテーマで研究をしてきましたが、学校教育で算数を学ぶ意義は何なのかは、私なりの大きなテーマでした。これまでの研究を通しての私の見解を10個に整理しました。
第7回は「見通しをもって生活するため」です。今回は、実践予定の指導案とともに紹介させていただきます。

東京都品川区立学校　平野　正隆

はじめに

教師は「なぜ算数を学ぶのか」という学習の意義を理解したうえで授業を構成することが大切です。そうすることで「何を学ぶか」だけでなく、「どのように学ぶか」にも目を向けた授業改善が可能になります。また、児童自身も学ぶ意味を実感しながら取り組むことが必要です。点数や順位などの比較にとらわれ、本来大切にすべき学びの方向性を見失っている子もいます。算数は単に難問を解いたり高得点を取ったりするだけではなく、学ぶ過程で培われる「生きてはたらく力」を育む教科であることを忘れてはなりません。

見通しをもって生活するため

算数では、問題を解決する前に、生活経験や既習事項を想起して、見通しをもってから取り掛かります。

例えば、５年生「速さ」の単元で考えてみます。7秒で40mと8秒で45mでは、どちらが速いのかというように、２つのものの速さを比べるとき、「時間」か「道のり」がそろっていなければ比べることができません。そこで、「単位量あたりの大きさ」や「平均」などの学習を想起し、そろえれば比べられるという見通しをもって課題解決に取り掛かります。

このような見通しをもっておくことは、日常生活でも大事です。例えば、家などの大きな買い物をする際に、貯金を毎月どのくらいすれば頭金がいつまでに貯まるのか、その後のローンはどのくらいになるのか、だから今はどんな生活をするべきなのか、というようにこれまでの経験をもとに未来から逆算して今を考えることができます。

指導の工夫(「割合⑴」第５学年)

①日常生活からの導入で、興味・関心を喚起する

本時で扱う、飛行機の混み具合を考えるにあたって、導入で冬休みの旅行や飛行機の話題を出し、児童にとって身近な話題（「家族旅行」「飛行機に乗る」など）と関連付けます。その中で「混み具合」という日常的に感じるが定量的に捉える機会の少ない概念に焦点を当て、子どもの「もっと知りたい」という探究心を自然に引き出します。

②教師が与えるのではなく、必要な情報を児童に気付かせる

「乗客数」「定員」など、混み具合を比べるために必要な情報を、教師が一方的に与えるのではなく、児童の問いや発言を通して徐々に引き出します。「空席はいくつありますか？」「面積が分かればいいのに…」といった発言を活用しながら、児童が「割合」という考え方に至る道筋をつくります。このように、児童自身が課題を構造的に理解するプロセスを支援することで、見通しをもって自力解決へ向かえるようにします。

③複数の考え方を示すことで、自分の方法を選ぶ見通しを与える

「数直線」や「四マス関係表」といった複数の表現方法を児童が発表する構成となっており、児童は自分が理解しやすい・納得しやすい方法で考えることができます。どちらも同じ「117÷130」や「442÷520」につながることで、どの方法でも正解に至ることの安心感と見通しを与えます。

指導案「割合⑴」(第５学年) 学校図書「みんなと学ぶ小学校算数５年」

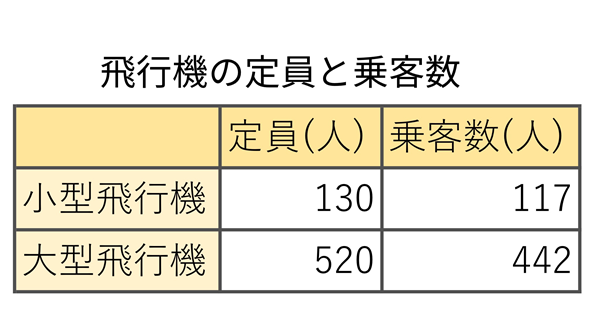
飛行機の定員と乗客数

※キャラクターカードとは、学校図書「みんなと学ぶ小学校算数５年」に出てくる考え方モンスターのことを指します。

【導入】

教師：みなさんは冬休みにどこか出かける予定ある？
児童：おばあちゃんの家に行くー
児童：家族で北海道に旅行に行く

教師：なかには飛行機に乗る人もいると思います。今日は、そんな飛行機の混み具合について考えていきます。

※写真等を見せ、日常生活の一場面を想起させながら、算数の問題へつなげたい。

児童：大きさが違う。

教師：そう。大型飛行機と小型飛行機です。中を図に表したのがこれです。（図では、黒マス＝乗客、白マス＝空席として表示）
児童：黒マスは何？白マスは？

教師：黒マスは乗客が乗っていて、白マスは空席です。どっちが混んでいますか？
児童：乗客は何人乗っているんですか？

教師：大型飛行機には442人、小型飛行機には117人が乗っているようです。
児童：大型飛行機すごい！
児童：442人も乗っているのなら、大型飛行機の方が混んでいるんじゃないかな？
児童：先生、それぞれの面積はどのくらいですか？

教師：面積がわかれば混み具合を求められそうですか。
児童：はい。人数÷面積をすれば1平方メートルあたりの人数で比べられます。

教師：面積は残念ながら分かりません。
児童：じゃあ、全部で何人乗れる飛行機ですか。
児童：空席はいくつありますか。

※教師が一方的に提示するのではなく、混み具合を比べるためには「乗客数」「定員」が必要であることを子どもたち自身に気付かせたい。

教師：定員のことですね。大型飛行機には520人、小型飛行機には130人乗ることができます。(ここで、表を提示する)
児童：定員が違うから同じにすれば比べられるんじゃないかな。

【自力解決】自由探究学習

めあて：こみぐあいの比べ方を考えよう。

※自由に探究・交流できる時間を設け、個に応じた学び方を選択できる場を大切にしたい。

【集団検討】対話的説明

※聞き手に問いかけたり、助けてもらったりしながら考えを伝える(発表する)対話的説明を取り入れたい。

考え方①（数直線を使った方法）

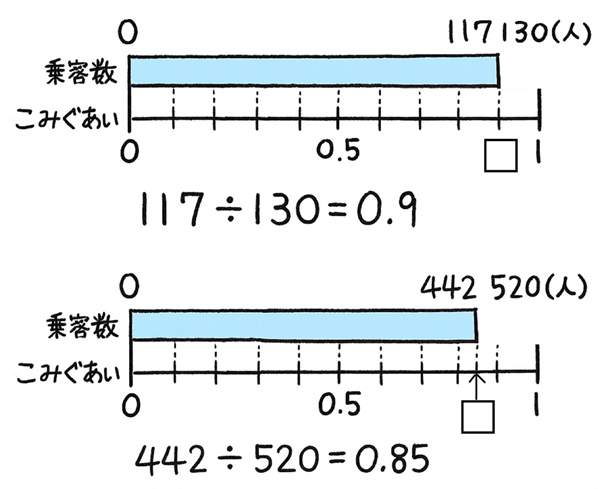
数直線を使った方法

教師：私は数直線にして考えました。まず、こちらは小型の飛行機です。定員が130人、そのうち117人が乗っています。青い部分が表しているのが何か分かりますか？
児童：乗っている人の数

教師：そうです。では、白い部分は？
児童：空いている席

教師：そうです。私は定員を1にして考えました。すると、定員を1にしたときの乗客数はどんな式になりますか？
児童：ヒトッツだ！(※教師がキャラカードを貼る)
児童：117÷130

教師：で、商は？
児童：0.9

教師：これは、ほとんどの席がうまっていることがわかります。次に、こちらは大型の飛行機です。定員が520人、そのうち442人が乗っています。同じように考えて式に表すと？
児童：442÷520

教師：商は？
児童：0.85

教師：こちらもたくさん乗っていますが、0.9よりは少ないです。つまり、混んでいるのはどっちですか。
児童：小型飛行機の方が混んでいます。

教師：そう、小型飛行機の方が混んでいると分かります。

考え方②（数直線を使った方法）

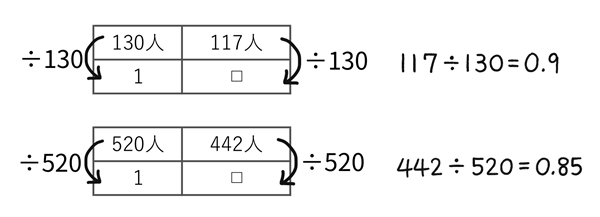
数直線を使った方法　

教師：私は四マス関係表にして考えました。
児童：ベツアラワシだ！(※教材に登場するキャラクター名。教師が対応するキャラカードを貼る)

教師：まずは小型飛行機です。四マス関係表の左上に「定員130人」、右上に「乗っている人117人」と書きます。下の段には、全体を基準とした割合を考えるので、下の左側には何と書けばいいですか？
児童：1

教師：定員130人に何をしたら1となりますか？
児童：÷130

教師：では、下の右側を求めるために117人をどうしたらいいですか。
児童：117÷130

教師：をすれば求められますね。計算すると？
児童：0.9

教師：つまり、全体1のうち0.9くらいの人が乗っているということです。
同じように、大型飛行機も見てみましょう。定員520人、乗っている人は442人です。
定員520人に何をしたら1となりますか？
児童：ソロエだ。1で揃えてる！！(※キャラクター名。教師がカードを貼る)
児童：÷520

教師：では、下の右側を求めるために442人をどうしたらいいですか。
児童：442÷520

教師：計算すると？
児童：0.85。

教師：つまり、全体1のうち0.85くらいの人が乗っているということになります。では、混んでいるのはどっちですか。
児童：小型飛行機の方が混んでいます。

教師：そう、小型飛行機の方が混んでいると分かります。混み具合を調べるとき、数直線を使った考え方にも、四マス関係表を使った考え方にも、117÷130と442÷520が出てきました。これを言葉の式にしてみましょう。
児童：キマリンだね。(※キャラクター名。教師がカードを貼る)
児童：乗客数÷定員数=混み具合
児童：一部の数÷ 全体の数=割合

教師：乗客数や一部の数を「比べられる量」と言い、定員数や全体の数を「もとにする量」と言います。そして、混み具合のように全体に対する一部の大きさを表すときに「割合」を使います。つまり…「割合=比べられる量÷もとにする量」となります。

【まとめ】

児童：混み具合は割合を使って表すことができる。
児童：数直線や四マス関係表を使えば、混み具合の割合を求められる。
児童：割合は、比べられる量÷もとにする量で求められる。

【振り返り】

児童：もとにする量(全体)を1として考えることで、それに対する比べられる量(一部分)の割合を求めることができる。

終わりに

本指導案の実践を通して、児童が生活の中で算数の考えを生かし、見通しをもって行動する力を育んでいきたいです。単に問題を解く力を育てるのではなく、「なぜその考え方が必要なのか」「どのように使えばよいのか」といった数学的な見方・考え方を、児童自身が意味づけながら獲得していく過程こそが重要だと考えています。今回扱った「割合」は、日常生活においても頻繁に用いられる概念で、それを自分の言葉で説明し、他者と対話を通して理解を深めていくことで、主体的・対話的な学びが実現します。

教師は、児童が「自分の生活と算数のつながり」を実感できるような導入の工夫や、学習過程での問いかけ、考えの交流の場づくりに常に意識を向ける必要があります。単元の学習を通して身に付けた見通しをもって考える力は、将来の生活や社会の中でも生きてはたらく力となります。今後も、児童の思考の流れや問いを大切にしながら、算数の学びが生活とつながる授業づくりを進めていきたいです。