2021.05.29

算数科　つまずきを乗り越える授業づくり〜見方・考え方のよさの実感〜（６）

子どもたちに、使える知識・技能を身に付けさせるためには、同じ見方・考え方を働かせていることの自覚を促すことが必要である。前回の記事はこのような内容でした。

今回は、自在に使える道具とするためには、その道具のよさを実感する必要があるということをお伝えします。

名古屋市立御器所小学校　教諭　松田翔伍

１　誤答にもよさがある

５年「小数のかけ算」の導入で、「１mの値段が80円のリボンがあります。このリボン2.1mの値段は何ですか」という問題を扱い、80×2.1の計算の仕方について学習した時のことです。
個人で考える時間を取ってみると、数人の子どもが「80×２＋10＝170」という間違いをしていました。読者の皆様ならどのように授業されますか？
私は、「このように考えている人がいました」と言ってそのまま式を黒板に書きました。すると、別の子どもから「え〜！ちがう！」という声が出てきました。

「どのように考えたと思いますか？」と尋ねると、数人の子どもが黒板の前まで出てきて、「２mと0.1mに分けたんだと思います」「そうそう」「でも、0.1m分の値段を求める時に、10にしちゃったんだと思います」と誤答であるわけを説明してくれました。
このような誤答でも、整数と小数に分けて考えるというよさが含まれているのです。この考え方を全体で共有しました。0.1m分の値段を求めるためには、80÷10＝８とすることを図を使ったり、実際のテープを使ったりして共有していきました。
その後で、「どうして分けて考えようと思ったの？」と発想の源を問いました。発想の源を問うことについては、加古希支男先生の『発想の源を問う』（2019、東洋館出版社）に詳しく書かれています。さて、そのように問うと、「分かりやすいからです」とよさを言葉にしたので、「どこが分かりやすいの」と突っ込みます。「小数の計算ではなくて、整数の計算になっているからです」と発想の源を引き出すことができました。

２　きれいに流れる授業は、よさが実感できていない？

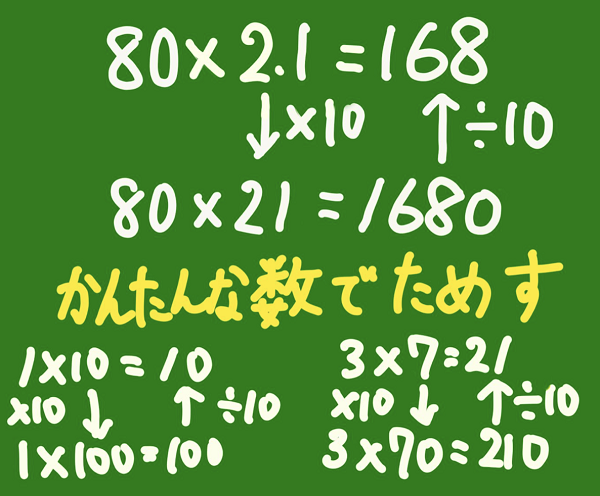
かけ算の性質を簡単な数で試す

もう一つ考え方を紹介します。図をご覧ください。いわゆる、かけ算の性質を使った考え方です。これも先程のような流れで、「習ったことが使える」「分かりやすい」というよさを引き出すことができました。
でも、浮かない顔をした子も数人いました。よさを実感できていないのです。するするときれいに流れていく授業は、よさの実感に至っていないのかもしれません。私自身の授業の話ですが。
そこで、私は「10倍して、÷10したら本当に答えが求められるの？」と突っ込みました。理解がゆっくりな人の役を演じたのです。うまく説明できない子どもたち。

私は、「簡単な数に置き換えて説明できますか」と投げ掛けました。そして、全員のノートに、自分が簡単だと思うかけ算の式を書かせ、かける数に10倍した式を計算させ、その積を10で割らせました。「積が元に戻るね」と新しいものを発見したかのような声も聞こえてきました。
私は、「10倍の時って、すごい性質があるんだね！」と言いました。「いや！100倍、1000倍もできる」「２倍もできるよ」「いやいや、何倍でも成り立つよ」と、かけ算の性質の適用範囲を広げていくような発言を引き出せました。
ここから、さらに実験させて成り立つことを確かめていきました。