2021.02.08

算数科　つまずきを乗り越える授業づくり（１）

学校では、「つまずき」という言葉を、否定的な意味で使うことが多くあるように思います。「あの子は、かけ算でつまずいているね」「あの子は文章題の読み取りでつまずいているよ」と、教員間で話題になることも多いです。実際、４月に出会う子どもたちは、間違えることを極端に隠したり、間違いを素直に認めなかったりすることで、つまずいていない自分でいようとします。『教室はまちがうところだ』（蒔田晋治・著、長谷川知子・イラスト、子どもの未来社）といくら言葉で伝えても、間違えるのは悪いことだという価値は根強く人の心の中に巣くっているのです。しかし、つまずきは悪いことなのでしょうか。本稿からは、子どもの「つまずき」に焦点を当て、「つまずき」とどう向き合えばよいのか考えていこうと思います。

名古屋市立御器所小学校　教諭　松田翔伍

つまずきの心理学的原因

つまずきは、過去から教育に携わる人々の関心の的でした。手元に『つまずきを生かす授業』（駒林邦男他著、1983年、明治図書）があります。その中から、つまずきの心理学的原因を引用してみます。　

*********************************

①　前提となる知識・技能の欠如による、つまずき
②　生活的概念・実地的一般化にもとづく、つまずき
③　認知構造の防衛機制による、つまずき
④　学習能力にもとづく、つまずき

*********************************

何やら難しい言葉が並んでいます。１つずつ分かりやすく、私の経験を交えながら説明します。

①　前提となる知識・技能の欠如による、つまずき

これは、かけ算の知識がないとわり算でつまずくということです。算数は系統性の強い教科です。積み上げがされていないと、上位の問題群は解けないということです。

②　生活的概念・実地的一般化にもとづく、つまずき

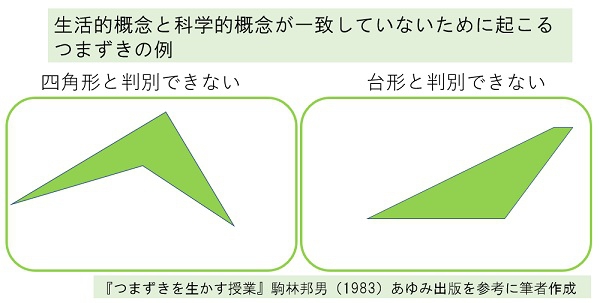
生活的概念の対となる概念は、科学的概念です。日常生活の中で習得する概念を生活的概念と捉えてよいでしょう。「一般化」とは、複数の事物、現象の間にある共通なものを一定の観点から取り出す頭の働きのことです。幼い子どもが犬を見て、「ワンワン」と指差せるのは、保護者が、「あれはワンワンだよ」「これもワンワン」と言って現実のものと言葉を結び付けているからです。次第に、耳があって、毛むくじゃらで、ワンと吠えるのが「ワンワン」と一般化していくことで、犬という概念を習得していきます。実地的一般化は、この例のように日常生活の中における一般化のことを指しています。

では、②のつまずきは算数の学習ではどのように表れるのでしょうか。例えば、くさび形の図形を四角形と判別できなかったり、細身の台形を台形と判別できなかったりするつまずきがあります。「向かい合う１組の辺が平行な四角形が台形」と教えているにも関わらず、台形と判別できないのは、「台」という言葉のイメージと、学校で学ぶ科学的概念としての台形がかけ離れているからでしょうか。台形を「一平行四辺形」、平行四辺形を「二平行四辺形」という名前にしていたら、このようなつまずきは少なくなっていたかもしれません。

③　認知構造の防衛機制による、つまずき

この分類は、ピアジェの思考発達論について理解しなければなりません。ここでは、私の解釈だけ述べさせていただきます。私が３年生の子どもを担任した時のことです。「１ｍのテープを1/2にすると何ｍですか」と問うと、「1/2ｍ」と答えます。「半分だから50㎝だね」ということも確認しました。その後で、「２ｍのテープを1/2にすると何ｍですか」と問います。ここでも「1/2ｍ」と答える子どもが大勢いるのです。「２ｍを半分にするのだから、1/2ｍではおかしいのではないですか」と、このように反論する子どももいます。それでも、「1/2にしたのだから1/2ｍです」と納得しない子もいるのです。このような例は、私が受け持った教室だけではなく、全国の教室であるのではないでしょうか。このようなつまずきは、1/2という分割・操作する意味と、1/2ｍ＝50㎝といった量を表す意味が混同していることで起きるつまずきです。先ほどの「1/2にしたのだから1/2ｍです」は、分割・操作する意味で分数を強く認知しています。まさに、「子どもの論理」と言うべきでしょうか。大人ならすんなり納得できることも、子どもにとっては納得できないという例は他にも多くあるでしょう。これによって起こるつまずきがこの分類に入ります。

④　学習能力にもとづく、つまずき

村井敏宏氏と山田充氏によれば、次のような能力が算数の理解に関わっていると言います。

*********************************

（１）　数概念形成（基数・序数性）
（２）　継次処理能力、同時処理能力
（３）　視覚認知、聴覚認知
（４）　言語の発達、偏り
（５）　ワーキングメモリ機能、記憶
（６）　プランニング
（７）　注意、集中

（『学びにくい子への「国語・算数」つまずきサポート』村井敏宏、山田充、2015年、明治図書）

*********************************

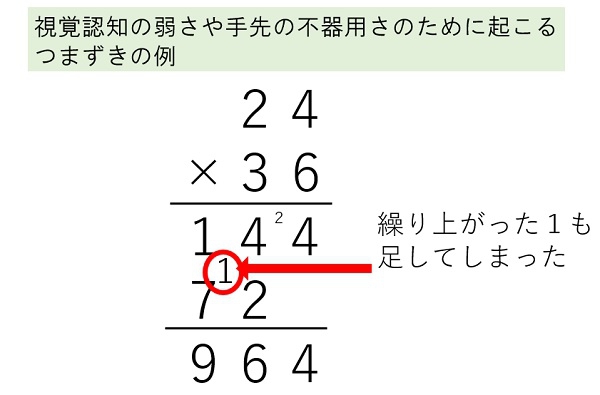
知的な遅れが算数のつまずきにつながっている場合も多くあります。知的な遅れがなくとも、（１）～（７）のどの能力が弱いのかという視点は必要でしょう。これらの視点以外にも手先の不器用さなどにつまずきがあることもあります。例えば、図のように筆算を誤ってしまったとします。これは視覚認知の弱さや手先の不器用さが原因だと考えられます。この場合は、縦に線を引くことを教えたり、繰り上がった数に〇を付けて目立たせる工夫を教えたりすることで、つまずきが減る可能性があります。

興味関心のつまずきも

①から④まで、つまずきの分類について考察してきました。これらの他にも、「興味関心のつまずき」もあります。（『社会科の「つまずき」指導術』宗實直樹著を参考）つまずくということは、間違えるということです。成功体験より間違える経験を多く積んだ子どもたちは、算数を好きになるはずがありません。「どうせ解けないから」「私には難しいです」と言って、問題に取り掛かる前にあきらめてしまうという姿を見たことはないでしょうか。そのような意味で、興味関心のつまずきは、様々なつまずきの結果であり、総合的なつまずきと言えるのかもしれません。子どもたちは、つまずきを否定的に捉えています。では、もしも、つまずいて良かったと思う経験を多く積ませることができたとしたら、どうでしょうか。否定的だったはずのつまずきを肯定的に見られるようになったとき、子どもたちは算数の学習で「楽しい」と思えるのではないでしょうか。