2025.05.07

愉しい授業を創る ― 多様な考えを交流させる編

「愉しい」授業は、どのように創ればよいでしょう？と問われたら、どのように応えますか。
人それぞれ異なるでしょうけれど。せっかく友達と一緒に学ぶのですから、自分には思いつかなかった多様な考えに触れられることも、愉しさの一つですよね。
自分の考えが、AからBに変容する、それこそが学びだと思うのです。
そんなところにも授業の愉しさがあると思います。

浜松学院大学地域共創学部地域子ども教育学科教授　川島　隆

授業をやったら、なんかよかった！

子どもたちが授業で学ぶことってどんなことか？
その答えの一つに、自分の考えが広がったり、深まったりすることじゃないかって思います。
授業のはじめと終わりで、何の変化もなかったら、その一時間は、何だったんでしょうってことになると思うのです。
同じ教室で、友達と学ぶ中で、
「あぁ、こんな考え方もあるんだ」
「そういうやり方もあるの！」
「それ、面白い！」
「だったら、こういうやり方もあるんじゃないか」
そんなふうに、いろいろな見方や考え方に触れること。
結果、「自分の考えが、やっぱりいいんじゃないか」
そうなる場合もあるでしょう。
でも、見方や考え方には、変容があった。
そう言えるんじゃないでしょうか。
「授業をやったら、なんかよかった！」
そう思えるのが大事じゃないかなと思います。

例えば、算数の授業ならば、

例えば、3年生の算数の授業。
こんな問題を、子どもたちに投げ掛けるとします。

えんぴつを4本買います。1本のねだんは、18円です。
代金は、全部でいくらになるでしょうか。

皆さんだったら、子どもたちが、どのように考えると思いますか？

「4×18」
「いや、これでは、４（本）×18（円）になる」
「それ、変だよね」
「18円のえんぴつが4本だから、『18×４』だよ」

そんなやりとりから、「18×４」の計算の仕方、筆算の仕方を考える授業にしていくでしょうか。
でも、それだけじゃ、あまり面白くないように思いますが、いかがでしょうか。

先ずは、図で考えてみたい！

図で考える

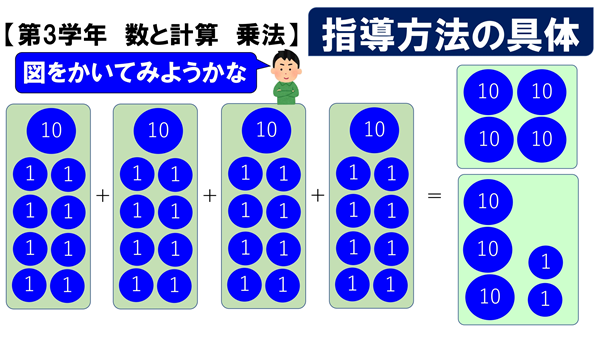
筆者作成

先ずは、図で考えてみたい。
問題を図で表せることは、問題の意味を理解していないとできません。
言い換えれば、図で表すことで、どのような問題場面かを理解することができます。

18円は、10円玉と1円玉で表現してみる。
それを4つ分合わせるということです。
つまり、10円玉だけを合わせて40円。
１円玉は、8枚が４組あるので、32円となり、

40＋32＝72（円）。

こうして、答えを導き出すことができます。

たし算で解いてみると

足し算で考える

筆者作成

たし算は、2年生で習っています。
ですから、単純に、➀　18＋18＋18＋18と式を書いて、順に足していくことを考える子どももいるでしょう。
また、「筆算、習ったな」と言って、②のようにノートに書いていく子どももいるかもしれません。
さらに、③のように、18という数字は、10と8を合わせた数であることに着目して解いていく子どももいるかもしれません。
1年生のときに、学習した「さくらんぼ計算」です。

いや、いや、かけ算でやってみたい！

掛け算で考える

筆者作成

「図やたし算じゃなくって、やっぱりかけ算でしょ」
という子どもも、もちろんいるでしょう。
でも、18をそのままでは、計算しづらい。
そこで、18を９＋9で考える子ども、10＋8で考える子どもが出てくるでしょう。
すると、④⑤のように、すでに学んだことを生かして計算できるのです。
どのような「さくらんぼ」で考えるとよいか。
そこがポイントですね。

たし算のように筆算で計算できないか

筆算で考える

筆者作成

「でも、もっと簡単に計算する仕方はないかな」
「たし算は、数が大きくなると、筆算をしたな」
ということで、かけ算の筆算のやり方へと考えを進めていきます。
⑥の考え方ですね。
この筆算の考え方は、先ほどの⑤の考え方と結び付くものですから、そのことに気付く子どももいるかもしれません。

もっと計算の仕方があるのかな？

工夫を考える

筆者作成

ここまで紹介してきたようにいろいろな考えを子ども同士が交流できたら、うれしくなっちゃいますね。
まさに、主体的に学ぶ子どもです。

さらに、こんな考え方もあるでしょうか。
例えば、18×4の計算の仕方を考えるならば、4×18だっていいわけですね。
このことは、九九でも経験ずみです。
すると、④や⑤の仕方が活用できます。

また、18は、20から2足らないという考え方ができたら、18＝20-2として、そこから（20-2）×4という計算の仕方もできるでしょう。
それを整理すれば、⑦のようになります。
これは、4年生の学習内容となってしまいます。
でも、そこにいきついてしまう子どももいるかもしれません。

結びに

ここで取り上げた問題は「18×４」。
つまり、（2位数）×（1位数）の計算が、乗法九九などの基本的な計算を基にしてできることを理解すること。
また、その筆算の仕方について理解することをねらいとするものです。

ただし、どのように理解をしていくか、その過程が大事だと思います。
単線型ではなく、いくつもいくつも解決の可能性や方法（仕方）を考え合って、これまで学習してきた内容を振り返りつつ、関連付けつつ、方法を見いだしていくことに意義や面白さがあるんじゃないかと思います。
自分の考えだけじゃなくて、友達の考えから学び、自分の考えを広げ、深める、AからBへの変容が実感できる授業ができるんじゃないかと思うのでした。

ちなみに、ここで示した指導法の具体は、「小学校学習指導要領解説　算数編」を参考にしております。
こうした指導の具体に踏み込んで、解説がなされているのです。
目の前の子どもたちだったら、どのように考えていきそうですか？
（3年生の問題ですが、4年生以上の子どもたちに投げ掛けてみたら、どう考えるのか。それもまた、愉しいかもしれません。）