学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
面積の求め方（第5回） ～同じ面積をみつけよう
図形の面積の問題では，見た目が違っても同じ面積ということがよくあります。今回は図形をいかにながめるかが大切です。難しい計算はありません。パズル感覚で気軽にチャレンジしてみてください。
問題
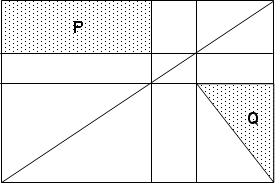
右の図のように，長方形に対角線を引き，たて，横それぞれに平行な線で区切りました。このとき，
（Pの面積）：（Qの面積）
を求めなさい。
◆ポイント
長方形を対角線で分けると，面積を2等分することに着目！
解法
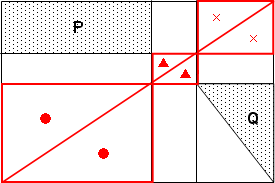
まずは，面積が同じになる部分に同じ印をつけてみましょう！
とりあえず，赤で囲んだ長方形の対角線に着目すると， ● ▲ × の面積が同じになることがわかります。
でも，これだけでしょうか？
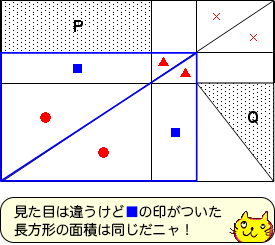
実はまだあります。もう少し大きく視点を変えて，青で囲んだ長方形に着目してみましょう。
青で囲んだ長方形は対角線で２つに分けられています。
長方形を対角線で分けると，面積を2等分します。 ●と▲を除くと長方形が残っています。この残った部分の面積も同じはずです。
すると，見た目は違いますが■で印をつけた長方形の面積も同じです。
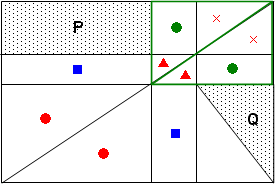
同じように緑で囲んだ長方形の●の部分の面積も同じです。
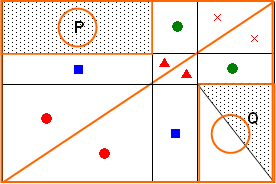
最後に一番大きなオレンジ色で囲んだ長方形に着目します。
印のついていない部分の面積は同じになるので， オレンジ色で大きく○をつけた部分の面積は同じです。
Qは○をつけた長方形の面積の半分の面積なので，Pの半分の面積になります。
よって
（Pの面積）：（Qの面積）＝２：１
となります。
この問題では小さな長方形から大きな長方形へ視点を変えながら，解いていきました。このように図形をさまざまな視点で見ることはとても大切です。
同じ要領で次のチャレンジ問題を解いてみてください。
答え：２：１
チャレンジ問題
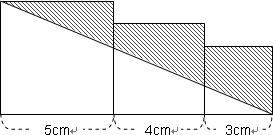
1辺が5cm, 4cm, 3cm の正方形を右の図のように並べました。このとき斜線部分の面積を求めなさい。
解法
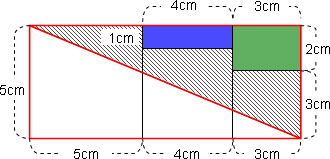
赤で囲んだ長方形の面積は
5×（5+4+3）＝５×12＝60cm²
対角線で分けた半分の面積は
60÷2＝30cm²
青い長方形の面積は
1×4＝4cm²
緑の長方形の面積は
2×3＝6cm²
よって，斜線部分の面積は
30cm²－4cm²－6cm²＝20cm²
答え：20cm²
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
