学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
面積の求め方（第1回）
前回までは，面積の考え方を長方形の面積（たて×よこ）をもとにして，平行四辺形や三角形，円やおうぎ形の面積の公式について説明しました。今回からは実践問題を通して，問題の解き方を説明します。図形の面積を計算する方法（ワザ）は数多くあります。これらをより多く覚えると複雑な図形の面積でも、簡単に計算できるようになります。今回は面積を求める公式がない図形の面積を三角形や四角形など公式が使える図形に分解することにより求める方法を説明します。
基本的な図形の面積の公式
問題1
次の図形について，斜線部分の面積を求めなさい。
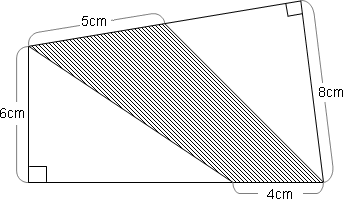
解法
面積を求めたい図形が，三角形や長方形などのように，単純な公式で面積が計算できないときは，求めたい図形を三角形や長方形など公式が使える図形に分けて考えるという方法があります。
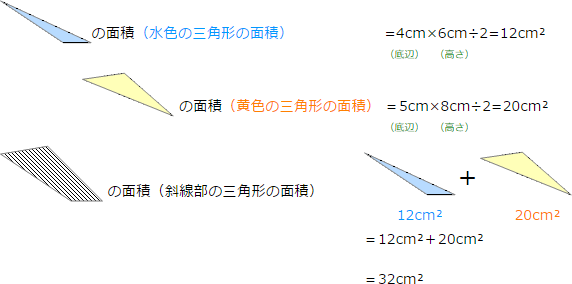
この斜線部の面積を求めるときには，次のように2つの三角形（水色と黄色）に分けて面積を計算して，２つの面積を合計することにより，斜線部の面積を求めます
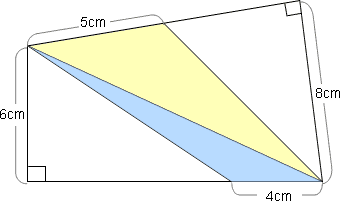
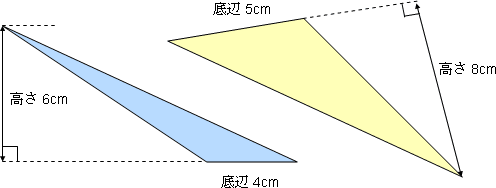
ところで，この２つの三角形の底辺は，水色が4cm，黄色が5cmですが，高さはわかりますか？
例えば，上の水色の三角形は斜めになっていてわかりにくいかも知れませんが高さは6cmです。黄色の三角形の高さは8cmです。
次の三角形は形が違いますが，どれも高さは同じで6cmです。ちなみに，面積は底辺×高さ÷2で計算するとどれも15cm²となります。
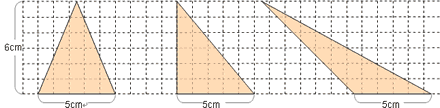
では，問題に戻って三角形の面積を求めてみます。
面積を求める基本ワザ１
公式ですぐに面積が求めることができない図形では，補助線を引き、底辺や高さがわかる三角形や四角形などに分けて計算し、合計して求める。
答え
32cm²
問題2
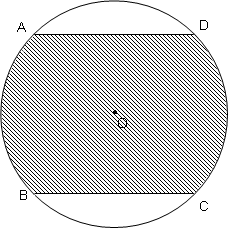
右の図の点A，B，C，Dは半径10cmの円Oの周を4等分した点です。斜線部分の面積を求めなさい。
解法
この斜線部の図形の面積もすぐには計算できそうもありません。
面積が計算できる図形に分けることができないかどうかを考えながら眺めてみます。
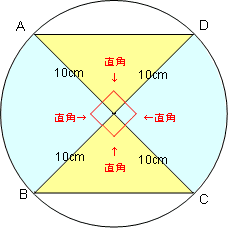
すると，右の図のように2つの三角形（黄色）と２つのおうぎ形（水色）に分解できます。
また，A，B，C，Dは円周を4等分した点なので，三角形は直角三角形で、おうぎ形の中心角は直角(90°)です。
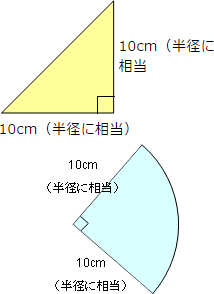
この円は半径10cmなので，直角三角形（黄色）は直角二等辺三角形です。
面積は
底辺×高さ÷2＝10×10÷2＝50cm²
おうぎ形は中心角が90°なので面積は
10×10×3.14× 41 =78.5
（円の面積の4分の1）
です。
斜線部の面積は
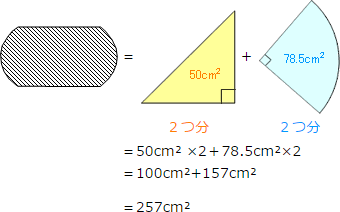
答え
257cm²
問題3
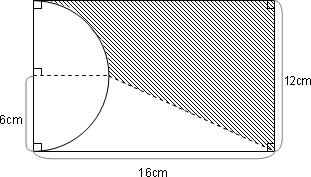
右の図の斜線部分の面積を求めなさい。
解法
これまでと同じように面積が計算できる図形に分けることができないかどうかを考えながら、斜線部分を眺めてみます。
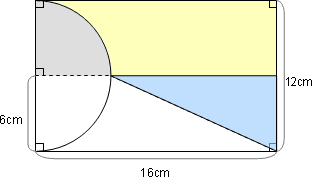
すると,右の図のように直角三角形（水色）と黄色の図形に分かれます。
直角三角形（水色）は公式で計算できそうですが，黄色の図形はすぐに面積を計算できそうもありません。
そんなときは，さらに細かく分けるか，引き算で計算できないか（より大きな図形から必要のない図形を引く）を考えます。
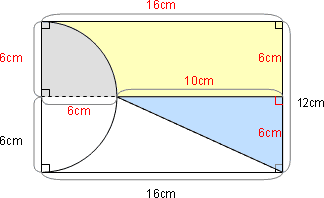
あらためてながめてみると，黄色の図形は上半分の長方形の一部になっています。
そしてこの長方形の左にはおうぎ形（灰色）があります。
つまり，上半分の長方形の面積をたて×よこで計算してから，おうぎ形（灰色）の面積を計算して，引き算をすれば，黄色の図形の面積を求めることができるのです。
それぞれの面積を計算する前に，長さのわかる辺は長さを記入していまいましょう。
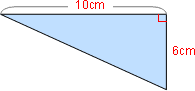
まずは，直角三角形（水色）を計算すると
6×10÷2＝60÷2＝30cm²
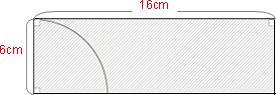
上半分の四角形の面積は
6×16＝96cm²
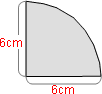
おうぎ形の中心角は90°で、面積は、円の面積の4分の1になるので
6×6×3.14× 41 =28.26cm2
黄色の図形の面積は、
96cm²－28.26cm²＝67.74cm²
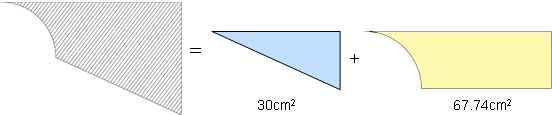
よって、問題の図の斜線部分の面積は、
直角三角形（水色）＋黄色の図形だから、
30cm²＋67.74cm²＝97.74cm²
面積を求める基本ワザ２
面積を求めるために、図形をうまく分けられそうもないときは、全体の面積から不要な部分の面積を引くことで求められることがある。
答え
97.74cm²
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
