学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
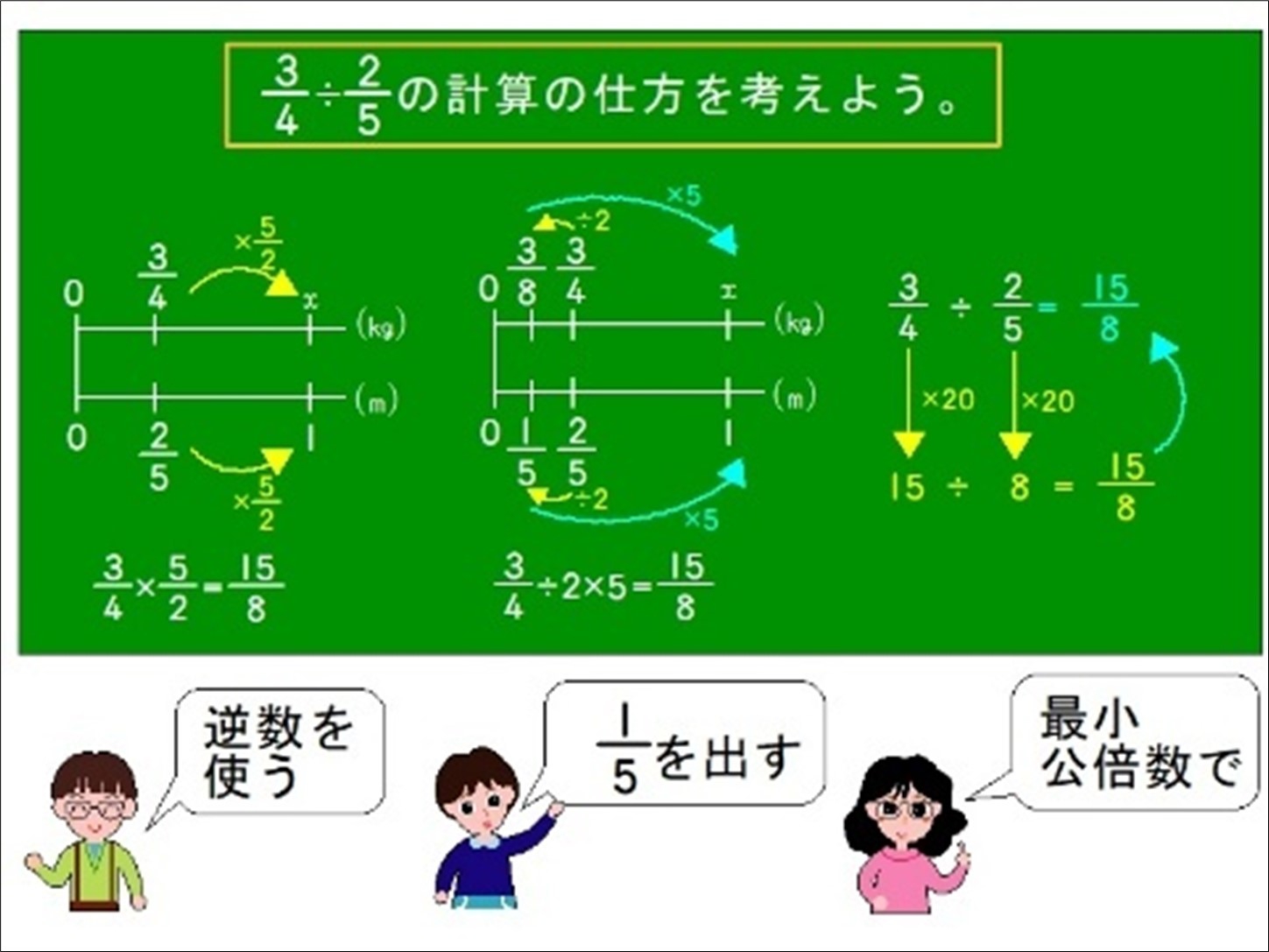
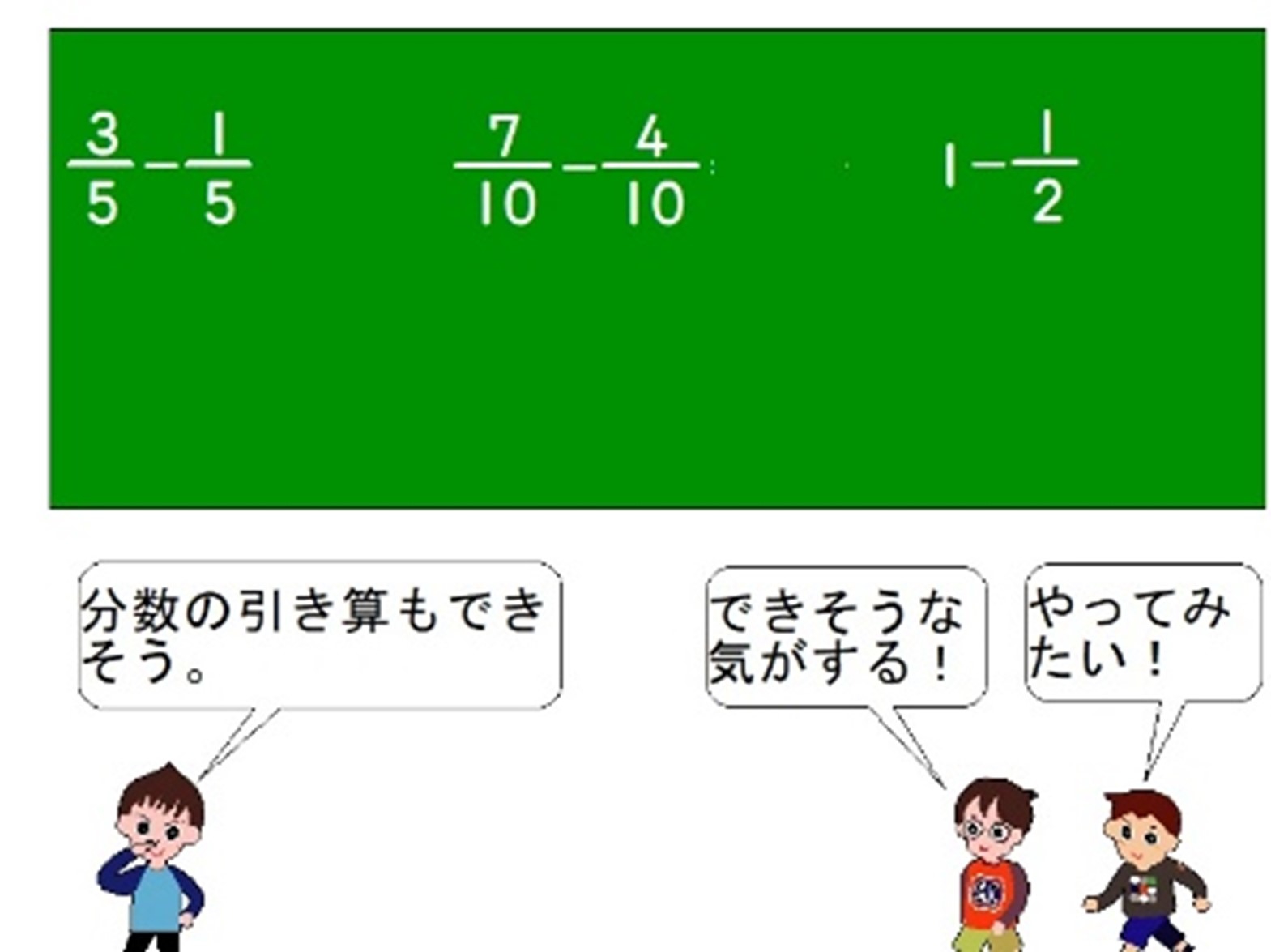
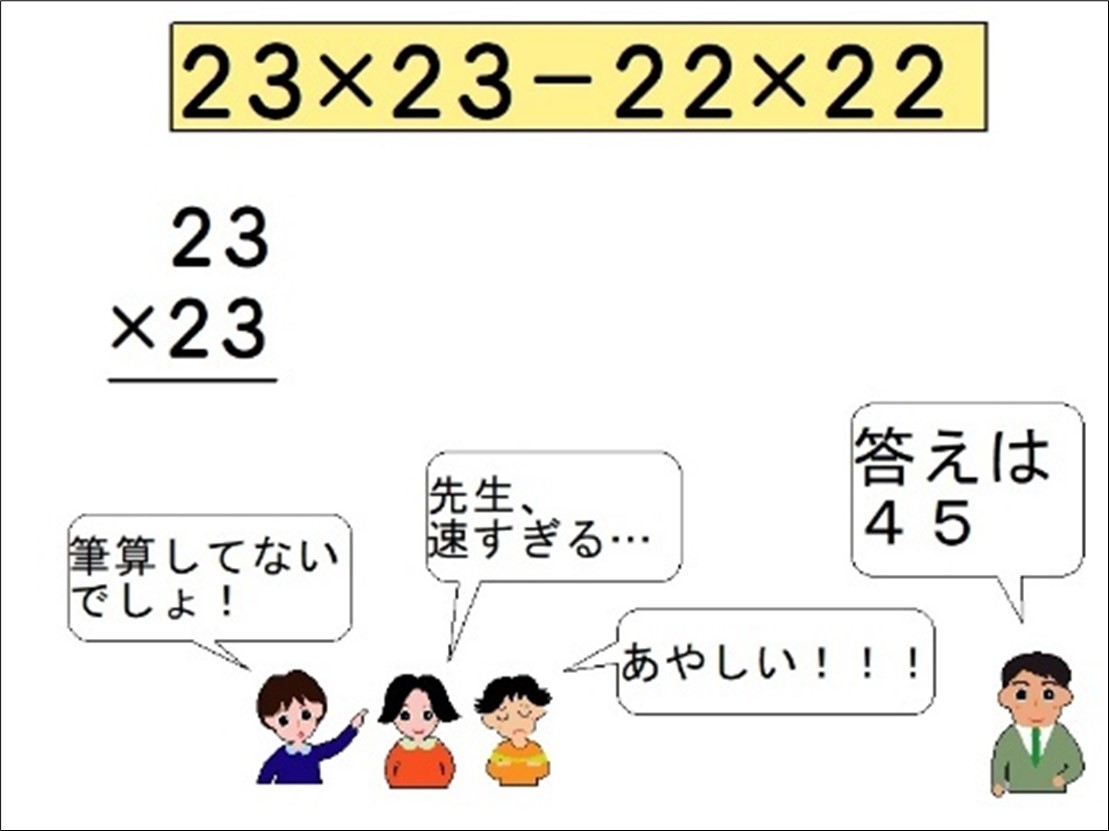
面積の求め方（第2回）
前回に引き続き、面積の求め方を説明します。面積の公式がない図形の面積を求めるときは、三角形や四角形など公式が使える図形に分解することにより求める方法がありますが、今回は図形を移動したり、組み合わせたりすることにより、面積の公式で計算できる図形にして求める方法を説明します。
面積の公式がない図形の面積を求めたいときには、補助線を引いて面積の公式が使えるいくつかの図形に分解してから、それぞれ公式をあてはめ、足し合わせるという方法で計算できることがあります。
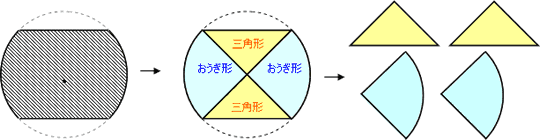
今回は図形を移動したり、組み合わせたりすることにより、面積の公式で計算できる図形にして求める方法を説明します（等積移動、等積変形の考え方）。
等積移動･･･面積を変えずに図形を移動すること
等積変形･･･面積を変えずに図形を変形すること
基本的な図形の面積の公式
問題1
次の図のような長方形の土地の中に畑があります。畑の中にはまっすぐで平行な道が交差しています。畑の部分の面積（黄色い部分）の面積を求めなさい。
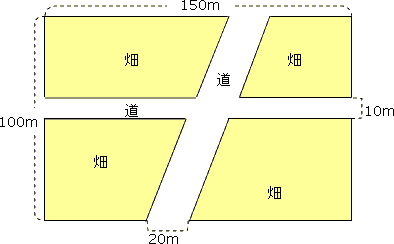
解法
この畑は複雑な形をしていますが、実は簡単に面積を計算する方法があります。
等積変形の考え方を使います。等積変形とは面積を変えずに形を変えることです。
上下に伸びている道の面積（平行四辺形）は、底辺×高さ＝20m×100m＝2000m²です。
これは、底辺が20m、高さが100mの長方形と同じ面積です。
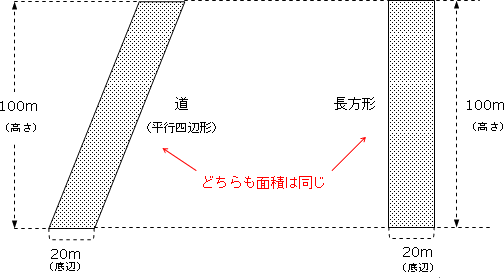
つまり、平行四辺形（底辺20ｍ、高さ100ｍ）は長方形（よこ20ｍ、高さ100ｍ）に等積変形できるのです。
問題文の図は次のように書きかえることができます（等積変形）。形が違いますが、道の面積も畑の面積も最初の図と同じです。
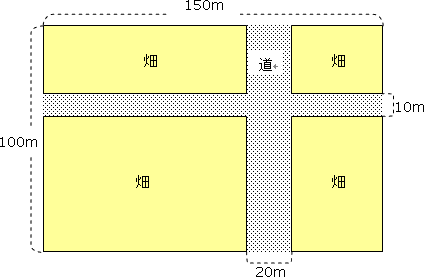
左右に伸びる道も同じように考えると、問題文の図は次のように書きかえることができます（等積変形）。形が違いますが、道の面積も畑の面積も最初の図と同じです。
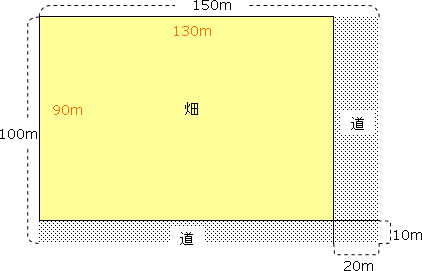
結局、畑の面積は、たて×よこ＝90m×130m＝11700m²ということになります。
答え
11700m²
問題2
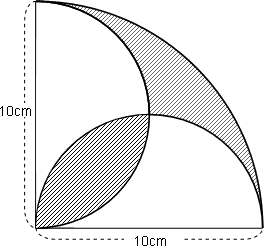
右の図は半径が10cmの4分円の中に、半径が5cmの2つの半円を描いたものです。円周率を3.14として斜線部分の面積を求めなさい
解法
第1問では、図形を等積変形したり、図形を移動したりすることによって面積を求める方法を説明しました。次の第2問も同じように、図形を移動することにより、面積を計算することができます。
この斜線部分も、すぐに面積の公式にあてはまる図形ではありません。補助線を引いて、単に分解しても面積の公式があてはまるような図形は出てきそうもありません。
そこで次の図のように、斜線部分の葉っぱ型の部分を2つに分けて、等積移動してみます。
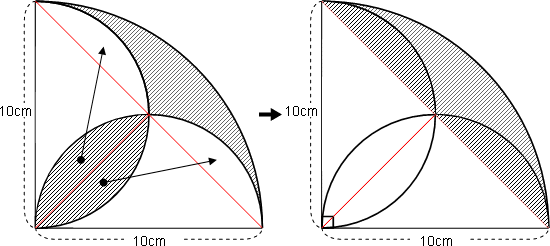
つまり、半径が10cmの4分円（おうぎ形）の部分から、斜線以外の直角三角形の部分を引けば、斜線部分の面積が計算できることがわかります。
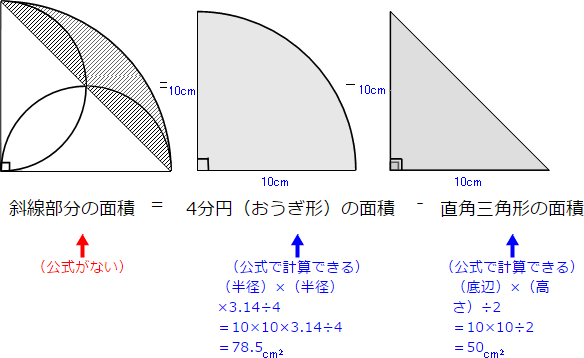
結局、斜線部分の面積は、78.5－50＝28.5cm²となります。
答え
28.5cm²
問題3
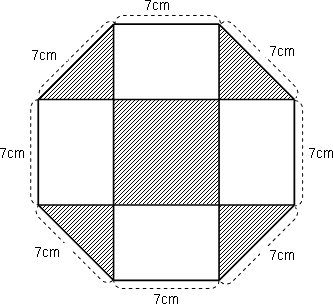
右の図は一辺の長さは7cm正八角形です。斜線部分の面積の和を求めなさい。
解法
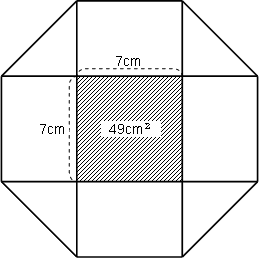
この斜線部分の面積のうち、真ん中の正方形の面積は、たて×よこの公式ですぐに計算できます。
7×7＝49cm²です。
四隅にある三角形はどうでしょうか？
それぞれ一辺のみ7cmということがわかっていますが、底辺も高さもわからないので、面積の公式にあてはめることができません。補助線を引いてもうまくいきそうもありません。
そこで４つの三角形（アイウエ）を次の図のように、組み合わせてみます。
面積も、たて×よこの公式で7×7＝49cm²と計算できます。
結局、最初の図の斜線部分の面積は、次の図のように、2つの正方形の面積の和になります。
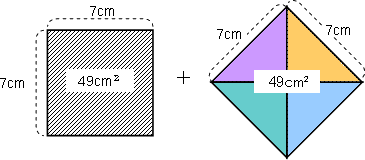
49 cm²＋ 49cmcm² =98cm²
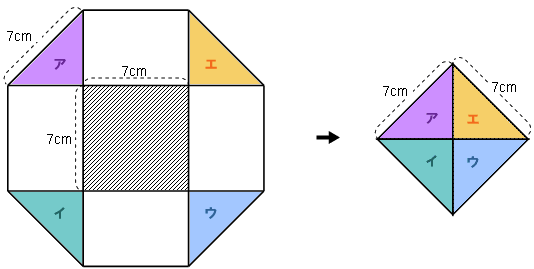
ア イ ウ エの４つの三角形を、取り出して組み合わせてみます
今回のまとめ
面積の計算をするときに、直接公式が使えないような図形のときは、分解したり、変形したり、移動したり、組み合わせたりして、面積の公式が使える図形にしてそれぞれ面積を計算し、足し算や引き算で考える。
答え
98cm²
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
