学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
面積の求め方（第4回） ～ロープでつながれた動物が動くことができる範囲の面積
今回はロープでつながれた犬や牛などの動物が動ける範囲の面積を求めます。結局はおうぎ形の面積の組み合わせです。必ず自分で図を書き，小数点を含む計算を行うことが必要で，知識よりもむしろ正確さと根気強さが大切です。
今回はまずは，おうぎ形の面積の復習から行います。
準備体操
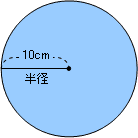
次の（1）～（4）のそれぞれのおうぎ形の面積は半径10cmの円の面積の何分のいくつになりますか。また面積は何cm²になりますか。円周率は3.14とします。
（1）中心角が90°のおうぎ形
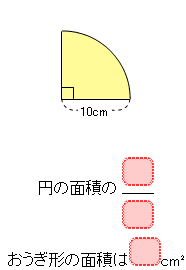
（2）中心角が180°のおうぎ形
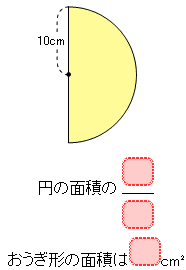
（3）中心角が270°のおうぎ形
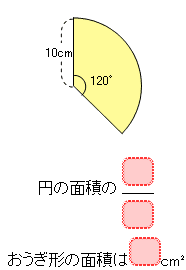
（4）中心角が120°のおうぎ形
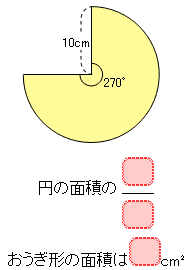
解説
おうぎ形の面積が円の面積に対してどれくらいの面積になるかは，図形をみれば直観的にすぐにわかるのものもありますが，基本的にはおうぎ形の中心角で計算します。
ここで，円の面積は（半径）×（半径）×3.14＝10×10×3.14＝314cm² です。
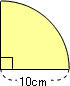
図を見れば，計算しなくても円の面積の4分の１に相当していることがわかると思います。計算では次のようになります。
360°90° ＝ 41
このおうぎ形の面積は
（円の面積）
314cm2 × 41 ＝ 314 × 41
＝ 314 ÷ 4
＝ 78.5cm2
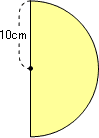
図を見れば，計算しなくても円の面積の２の１に相当していることがわかると思います。計算では次のようになります。
360°180° ＝ 21
このおうぎ形の面積は
（円の面積）
314cm2 × 21 ＝ 314 × 21
＝ 314 ÷ 2
＝ 157cm2
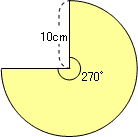
図を見れば，計算しなくても円の面積の4分の3に相当していることがわかると思います。計算では次のようになります。
360°90° ＝ 43
このおうぎ形の面積は
（円の面積）
314cm2 × 43 ＝ 314 × 43
＝ 314×3 ÷ 4
＝ 235.5cm2
中心角が120°なので，次のように計算します。
360°120° ＝ 31
このおうぎ形の面積は
（円の面積）
314cm2 × 31 ＝ 314 × 31
＝ 314÷ 3
≒ 104.7cm2
答え：(1)78.5cm² (2)157cm² (3)235.5cm² (4)104.7cm²
問題1
次の図のように，たて1ｍ，横3ｍの長方形の小屋があります。小屋のすみに2mのロープで犬がつながれています。小屋の外で犬が動ける範囲の面積を求めなさい。
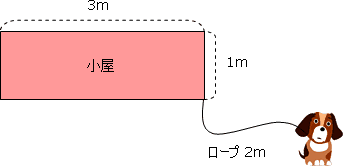
解説
動物（犬）が動くことができる範囲はロープが最大限に伸びているときの状況で考えます。小屋やさく，へいなどの影響で，場所により大小さまざまなおうぎ形ができます。
ロープがつながっている場所（点）や小屋やさく，へいなどの角（すみ）がおうぎ形の中心になります。ロープの長さも考えて中心となる点をみつけます。
この問題で，おうぎ形の中心になるのは，2箇所（ 
と 
）です。
ロープの長さは，2ｍなので，図の左側の2つの角は中心にはなりえません。
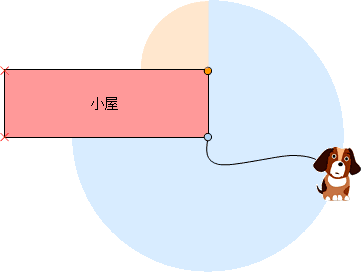
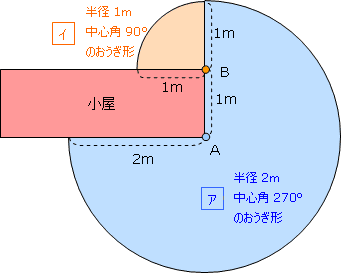
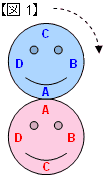
この問題では，２つの中心があり，２つのおうぎ形ができます。それぞれ分けて面積を計算して， 最後に足し算します。 まずは，水色のA点 から考えてみます。
ロープを最大限に伸ばした状況で考えます。
小屋のすみのロープでつながれている点を中心として，半径2m，中心角270°のおうぎ形 （水色）ができます。このおうぎ形の面積は半径2mの円の面積の4分の３に相当するから，
（円の面積）
2×2×3.14 × 43 ＝ 2×2×3.14 × 43
＝ 9.42m2
さらに，Ｂ点を中心としたおうぎ形は，半径1m，中心角90°のおうぎ形（オレンジ色）です。このおうぎ形の面積はは半径1mの円の面積の4分の1に相当するから，
（円の面積）
1×1×3.14 × 41 ＝ 1×1×3.14 × 41
＝3.14÷4
＝0.785m2
小屋の外で犬が動ける範囲の面積は，
9.42m²＋0.785m²＝10.205m²
答え：10.205m²
問題2
1辺が9mの正三角形のさくABCがあり，Aから3m離れたDに長さ12m のロープで牛がつながれています。この牛はさくの外側だけ動きまわることができます。牛が動くことのできる範囲は何m²ですか？
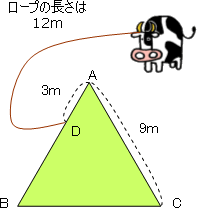
解説
この問題でおうぎ形の中心となりうる点は，D（）とA（
）とB（）です。ロープの長さが12ｍであることを考えると，C点を中心としたおうぎ形はできません（どんなにがんばってもC点までしか行けません）。
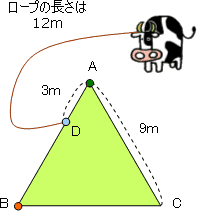
それぞれの中心に対して，牛の動くことができる範囲（おうぎ形）を書いてみます。
次の図のように３つのおうぎ形で表すことができます。
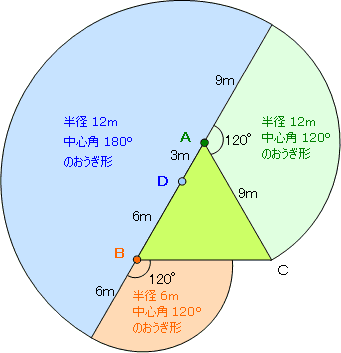
次にそれぞれのおうぎ形の面積を求めます。
Ｄ点を中心としたおうぎ形は半径12ｍ，中心角180°なので，面積は
（円の面積）
12×12×3.14 × 21 ＝ 12×12×3.14 × 21
＝226.08m2
Ａ点を中心としたおうぎ形は
（円の面積）
9×9×3.14 × 31 ＝ 9×9×3.14 × 31
＝ 84.78m2
Ｂ点を中心としたおうぎ形は
（円の面積）
6×6×3.14 × 31 ＝ 6×6×3.14 × 31
＝ 37.68m2
これらを足すと
226.08m² ＋ 84.78m² ＋ 37.68m² ＝ 348.54m²
答え：348.54m²
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
