2005.09.13

面積の求め方（第3回）～葉っぱ型図形の面積

前回に引き続き、面積の求め方を説明します。今回は「葉っぱ型」とか「レンズ型」などと呼ばれている図形の面積に関する問題です。葉っぱ型図形には面積の基本公式はありません。しかし、分解・変形・移動や足し算・引き算を意識しながらじっとながめてみると、ある図形が見えてきます。

左の図形は面積の問題でよく登場します。この図形はあまりによく見かけるので、「葉っぱ型」とか、「レンズ型」などと愛称がつけられています。
今回はこの図形の面積に関係する問題を説明します。

面積の問題を解くときの基本的な考え方

(1)　面積の基本公式の利用

面積の問題を解くときの基本は、公式にあてはめて計算します。ただし、すぐに公式にあてはめることのできる問題はほとんどありません。次の（２）のように工夫して公式にあてはめることのできる図形を作る必要があります。

(2)　分解・変形・移動

面積の問題のほとんどの問題は、すぐに公式が使えるような図形ではありません。そのようなときは、補助線を引いて分解して、組合せたり、（等積）変形したり、（等積）移動したりして、面積の公式が使える図形にします。

(３)　足し算・引き算

より大きな図形の面積を足し算などで求めてから、不要な面積を引くことにより、必要な図形の面積を計算するという方法です。

基本的な図形の面積の公式

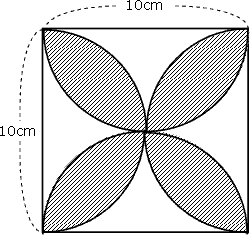
問題1

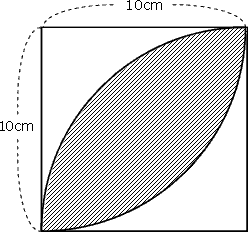
右の図の斜線部分の面積を求めなさい。
ただし、円周率は3.14とします。

解法

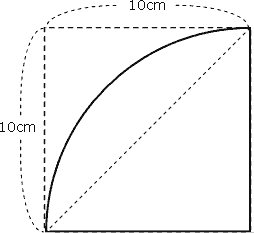
面積の問題の代表的な問題です。
この斜線部の葉っぱ型の図形は面積の基本公式にはありません。そこで、分解・変形・移動や足し算・引き算を意識しながら、じっとながめてみると、おうぎ形と直角三角形が見えてきます。
そして、次のように引き算すると、葉っぱの半分の面積が計算できるので、最後にそれを2倍します。

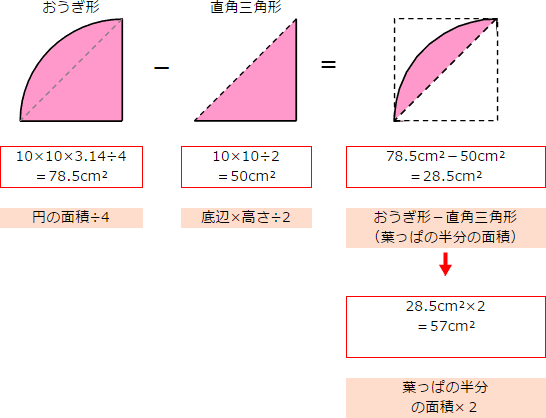
57cm²という結果は、正方形の面積100cm²の57％にあたります（正方形の面積の0.57倍）。
つまり、葉っぱ型の図形の面積は
（1辺の長さ）×（1辺の長さ）×0.57
でもとめることができるのです。
この公式を覚えておくと、問題を効率よく解くことができます。
ただし、円周率が3.14とした場合のみにあてはまる公式です。
（ちなみに、円周率が3.1のときの葉っぱの面積は正方形の55％、円周率が3のときは50％になります）。

面積の問題では考え方が大切です。この公式を使う場合は、必ず解説の解き方を理解した上で使いましょう。なお、ここではこの公式を「葉っぱ公式」と呼ぶことにします。

答え
57cm²

では、この公式を活用して次の問題も解いてみましょう。

問題2

右の図の斜線部分の面積を求めなさい。
ただし、円周率は3.14とします。

解法

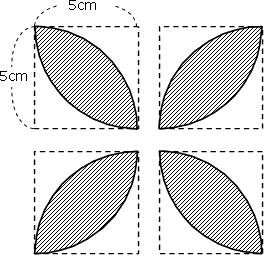
今度は、葉っぱが４つの四つ葉型の面積です。
葉っぱ1枚分の面積を求めて4倍すれば、四つ葉の面積になります。

右の図のように、四つ葉を分解して考えると、葉っぱ1枚が入っている正方形の一辺の長さは、5cmです。

葉っぱ1枚分の面積は、葉っぱ公式により

5cm×5cm×0.57＝14.25cm²

よって
四つ葉の面積は
14.25×4＝57cm²
です。

答え
57cm²

次は、前回(先月)の問題を葉っぱ公式を使って解いてみます。

問題3

右の図は半径が10cmの4分円の中に、半径が5cmの2つの半円を描いたものです。円周率を3.14として斜線部分の面積を求めなさい。

解法

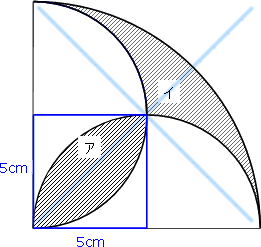
左下に小さな葉っぱ（ア）があります。
この葉っぱを囲む正方形は5cmなので，
5cm×5cm×0.57＝14.25cm²
です。さらに，残った右上の斜線部（イ）の面積を足せば答えがでます。
しかし，右上の斜線部（イ）の面積は，簡単には求めることができそうもありません。
別の方法を考えてみましょう

そこで、この小さな葉っぱを分解・移動して、次の図のようにします。
すると、大きな葉っぱの半分ができます。

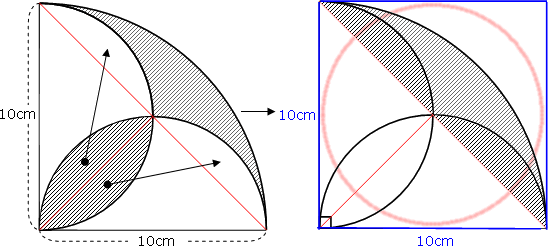
みかけは違いますが、どちらも斜線部分の面積は同じです。

この大きな葉っぱが入っている正方形の1辺の長さは10cmです。
葉っぱ公式を使うと

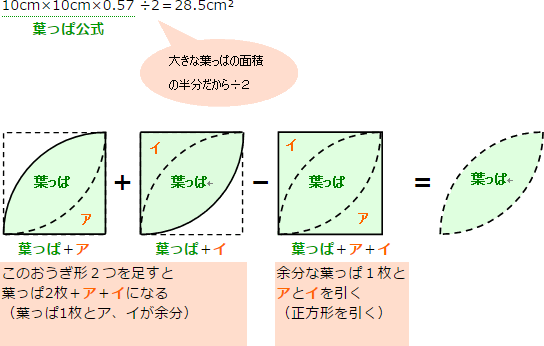
公式は便利ですが、このように足し算・引き算などを使って工夫しながら面積を計算する方法も大切な考え方です。

答え
28.5cm²

教え上手きんたろう先生

「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。