2026.01.22

図形の面積の公式化についての授業実践　〜「÷2の意味を考察する」から広がる理解〜

「ミスった。÷2するのを忘れてた......」「俺も台形で÷2を忘れた」

単元テストを返却したとき、教室のあちこちからこのようなつぶやきが聞こえてきました。5年生算数「三角形や四角形の面積」では、多くの子どもが一度は経験する場面です。計算自体は正しくできているにもかかわらず、「÷2をつけ忘れてしまう」。なぜこのようなミスは繰り返されるのでしょうか。

本実践では、この「÷2」に潜む意味を、子どもたち自身が公式をつくり出す過程を通して明らかにしていきました。公式を「覚えるもの」から「生み出すもの」へと位置付け直すことで、子どもたちの理解はどのように変容したのかを報告します。

東京都品川区立学校　平野　正隆

暗記した公式で解くから「÷2」を忘れる

そもそも、なぜ子どもたちは「÷2」を忘れてしまうのでしょうか。その背景には、公式を完成した形のまま暗記し、当てはめて使う学習にとどまっていることがあると考えられます。

公式が成り立つ理由や、どの数量をどのように扱っているのかを十分に理解しないまま学習が進むと、計算はできていても、式の一部を落としてしまったことに自分で気付くことができません。このような誤りは、単なる不注意ではなく、公式の意味理解が十分でないことの表れであると言えます。

そこで本授業では、公式の形を覚えることよりも、「なぜその式になるのか」「その式は何を表しているのか」を考える学習過程を重視しました。

公式化を自分たちで行う学習構成

著者作成

本実践では、公式を教師から与えるのではなく、子どもたち自身が公式を組み立てていく活動を中心に据えました。図形の面積を求める過程で用いた数値を、元の図形に含まれる底辺や高さ、上底・下底と結び付けて整理することで、その式自体が公式となることをねらいとしています。

ただし、いきなり完全な自力解決を求めるのではなく、次の二段階で学習を構成しました。

【ステップ１】平行四辺形・三角形は教師の支援のもとで公式化

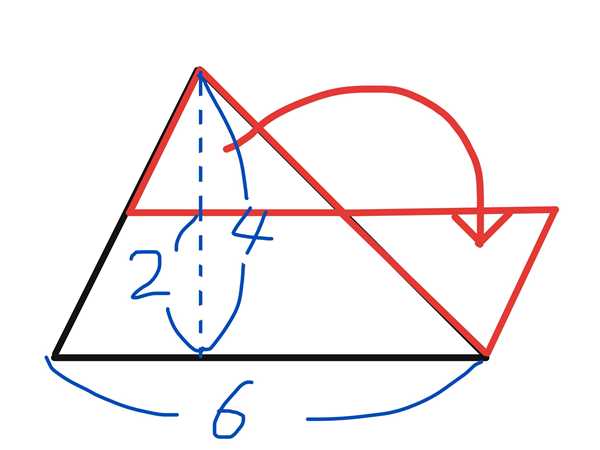
単元導入では、平行四辺形や三角形を扱いました。図形を動かしたり、補助線を引いたりしながら面積を求め、その数式について「もとの図形のどの長さを使っているのか」を問い返していきます。

例えば、ある子は三角形の面積を求める際に、式を「6×2」と表しました。6は三角形の底辺を表していますが、2という数値は元の図形には直接存在しません。そこで、この2がどこから生まれたのかを問い直すことで、高さが4cmであり、その半分であることに気付かせます。

このように、

6×2＝6×（4÷2）

という式の変換を通して、「底辺×高さ÷2」という公式へとつながっていきます。他の考え方でも同じ公式になるかを班で学び合いながら検討し、考えを統合していきました。

発表の場面では、「÷2は何を半分にしているのか」を問いかけると、「高さを半分にしている」「底辺を半分にしている」「面積そのものを半分にしている」など、さまざまな捉えが生まれました。最後に、「三角形の面積は底辺×高さ÷2で求められる」こととともに、「÷2の意味は考え方によって異なる」ことを学習のまとめとして共有しました。

【ステップ２】台形・ひし形は完全に自力で公式化

導入での経験を踏まえ、台形とひし形では教師の直接的な支援を最小限にし、子どもたち自身での公式化に挑戦させました。

個人や班での話し合いを通して、等積変形や倍積変形の考え方を用い、既習の図形に帰着させながら考えていきます。補助線の引き方一つで図形の見え方が大きく変わり、「上下に分ける」「左右に寄せる」「ひし形を二つに切って三角形として考える」など、多様なアプローチが自然に生まれました。

また、式に表す数値を、元の図形の辺の長さや高さで説明しようとする姿が多く見られるようになりました。式の違いが、どのような考え方の違いに対応しているのかを互いに説明し合う中で、公式化が「自分の考えの結晶」として意味をもち始めたように感じられました。

公式化の過程で気付く「÷2」の多様な意味

著者作成

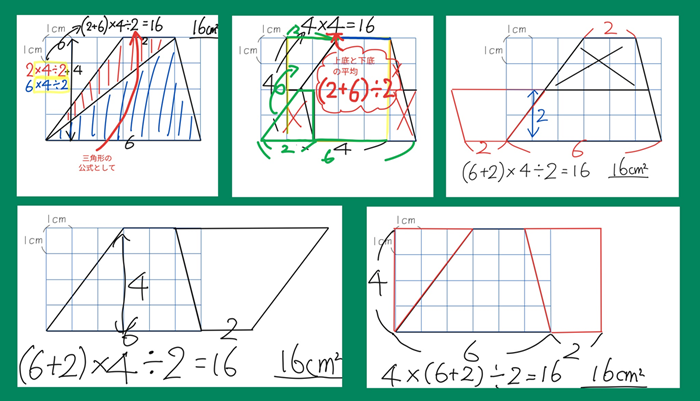
自分たちで公式をつくり出す過程を通して、多くの子どもが「台形やひし形でも、考え方によって÷2の意味が変わる」ことに気付き始めます。

例えば、台形を二つ合わせて平行四辺形にする倍積変形では、「÷2」は面積を半分にする操作として現れます。一方、三角形に分けて考える場合には、三角形の公式に含まれる「÷2」として現れます。また、図形をずらして平行四辺形に変形する等積変形では、高さを半分にしたり、上底と下底の平均を取ったりする意味として「÷2」が登場します。

このように、異なる見方や操作が、同じ公式へと収束していく体験は、子どもたちにとって数学の本質に触れる重要な機会となりました。公式とは一つの絶対的な答えではなく、多様な思考の結果として得られた共通の表現であることを、実感を伴って理解していったのです。