2024.02.07

５年生「面積」どっちから導入する？

５年生の算数で扱われる三角形、平行四辺形、ひし形及び台形の面積の計算による求め方の学習では、最初に三角形を扱うか、平行四辺形を扱うかは、教科書会社によって異なります。
では、なぜ違いが生まれるのか、その後の学習にどんな影響を及ぼすのでしょうか。

東京都品川区立学校　平野　正隆

⑴本単元で育成を目指す資質・能力

本単元を通して、図形を構成する要素に着目して、面積や体積の計算による求め方を考察する力を育成することを目指します。

５年生では、三角形、平行四辺形、ひし形及び台形の面積の「求め方を考える」ことを指導します。既習の形に分けたり、変形したりすることで面積が求められることを操作や図に表しながら確認し、図形の性質(向かい合う辺が平行、向かい合う辺の長さが等しいなど)を使った説明をしていきます。

⑵教科書会社による違い

令和2年度から5年度に使用されている教科書では、算数科教科書を扱う６社のうち、５社が平行四辺形から、１社が三角形から導入しています。
また、平行四辺形から導入している５社のうちの３社が、周りの長さが等しい長方形との面積を比較するところから単元の学習が始まります。

⑶平行四辺形から導入すると

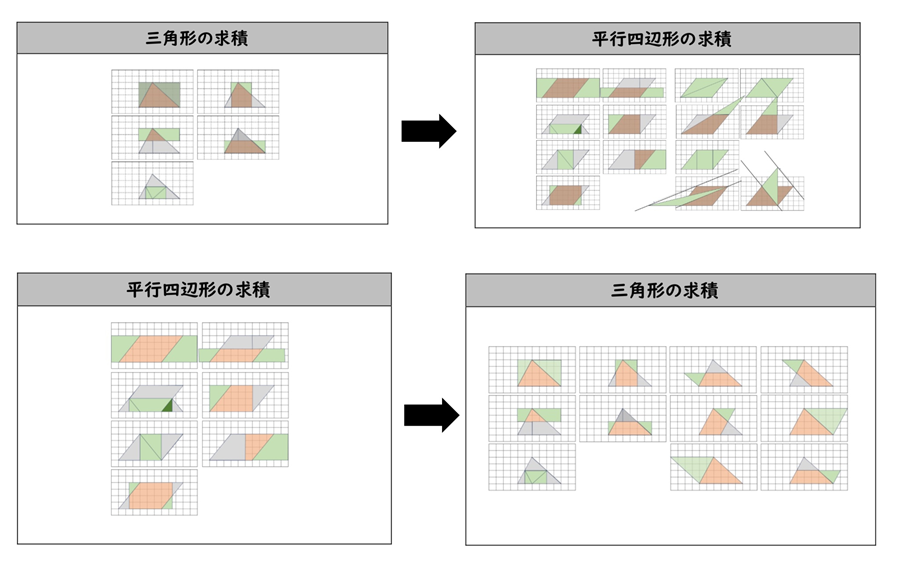
平行四辺形から導入する良さは何があるのでしょうか。

まず、長方形への等積変形がたくさんできるため、多様な考えを引き出せることが挙げられます。予測される考え方が、三角形で導入した場合は５通りであるのに対し、平行四辺形で導入した場合は７通りあります。

また、平行四辺形から導入すると、周りの長さが等しい長方形との面積を比較する場面から始めることができるため、面積を求める必然性をつくりやすいといえます。

さらに、三角形の面積を考える際、平行四辺形の半分と考えて求められます。これは、三角形の求積公式を導く際の÷2の意味理解に大きく役立ちます。三角形から導入すると、「÷2は底辺や高さを半分にしている」という考えしか出てきません。「平行四辺形の面積の半分だから÷2」という考えの方が、子どもたちは理解しやすいです。

しかし、平行四辺形から導入した場合、平行四辺形の求積でも、三角形の求積でも分解や頂点移動で、面積を求める考えに至りにくいです。そのため、台形やひし形の求積で、それらの考えを取り上げて理解を図る必要があります。

⑷三角形から導入すると

三角形から導入する良さは何があるのでしょうか。

四角形は三角形２つ、五角形は三角形３つというように、どんな多角形も必ず三角形に分割できます。また、平行四辺形の形をしたものは、身の回りにあまり存在していないのに対し、三角形は存在します。そんな、最も有用性が高い三角形を単元の最初に扱うことで印象に残すことができます。

さらに、平行四辺形の求積の際に、分割や頂点移動による等積変形の考え方を引き出すことができます。予想される考え方が14通りもありました。

しかし、三角形の求積公式を導く際に考える÷2の意味は、底辺や高さを半分にする考え方になるため、視覚的に捉えられるよう配慮する必要があります。また、平行四辺形の求積の際に「平行四辺形は三角形の２倍ということは、三角形は平行四辺形の半分である」と、図形を用いて理解したり、それが公式にも表れていることに気づかせたりすることも大切です。