2020.07.15

子どもの発問（発問研究 Vol.6）

ここに主語・述語に関する問題がある。

問題：次の文の主語を書きましょう。
文：（　　　）が発問を行う。
答え：教師

答えは、教師だけだろうか？
答えが、1つだけじゃないとすれば、他に何があるのか？
答えの可能性を、過去の記事を参考に、半径3m広げてみよう。

1.教師が、発問(問うべき問い、タイムマシン発問)を行う。
2.教師が、無言の発問を行う。
3.子どもが、発問を行う。

すると、このような答えが出てきた。本稿では、3つの目にスポットを当てる。
子どもが発問を行う。つまり、子どもが自ら問いをもち、問いを言葉で発すること。
「子どもの発問」ということができるだろう。

高知大学教育学部附属小学校　森寛暁

あなたは、子どもの主体性に蓋をする者が、誰か知っているのか？

いい問いは、たき火のようである。自然に人が集まり、話し合いが始まる。以前そう書いた。しかし、薪がないと、火は起こせない。薪を焚べないと、火は消えてしまう。そうだよね。

そのことに気づいた教師は、必死に薪を用意する。燃え具合を見取る。そして、必要と感じたときに新たな薪を焚べる。火を絶やしてはならない。そう思いながら。

ある日、薪を用意し、焚べ続けた教師は、ある違和感を覚える。たき火の周りにいる子どもたちの様子がおかしい──。教師が薪を用意するのをじっと待っている。教師が薪を焚べるまで、ずっと止まっている。まるで、誰かの指示がないと動けない指示待ち人間の亡霊のようだね。そんな声が遠くの空から降りてきそうなほどに。

だったら、何ができるか？　子ども自らが薪を用意し、焚べられるようにするには、教師は一体何ができるか。そう考えたい。そう自分自身に問える教師でいたい。そうだよね。

あらかじめ用意された「めあて」を毎時間教師に提示され続けた子どもが、自ら問いをもち、楽しみながら学ぶようになる日は、来るのだろうか。その答えは、ノー。

ねえ、早く気づいて。子どもの主体性に蓋をする者の存在に。

わたしは、子どもの主体性を引き出す者に、本当になりたいのだろうか？

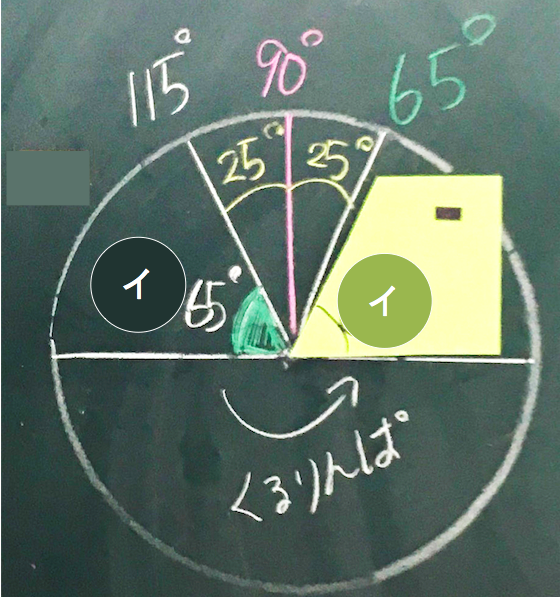
では、授業事例を1つ。4年生の算数「角の大きさ」。子どもたちが、「角度の測定」「分度器」などと初めて出会う場面である。わたしは、単元を通して、子どもが自ら問いをもって進めていけないか、と考えを巡らせていた。つまり、問いの連続を生みたかったのである。
結果は、途中で途切れてしまった。しかし、運良く問いが子どもの中で連続で起きた瞬間が何度かあった。生まれた問いがつながり、本時と次時をすぅーとつなげた。まるでリレーのバトンパスのように。

まず、角度の測定の授業中のこと。わたしは同時に2種の問題を提示した。子どもが使用する分度器は、右からと左からの両方向から測定可能である。子どもが分度器を線に合わせる。その瞬間、問いが生まれた。「どっち〜？」。アの角度は、60°か120°のどっちが正解なのか、イの角度は、65°か115°のどっちが正解なのか、という問いである。何度測定し直しても、同じ考えになった子どもは、「正直どっちでもいい！」と言い出してきた。しばらく悩んだが、「直角より大きいか？　小さいか？」と考えることで納得した。直角を基準として角の大きさを判断したのだ。だが、子どもたちは、0°の線を合わせた方の目盛りをよめばよいことには、まだ気づいていない。

子どもたちの分度器には、いつも2通りの数字が並んでいる状態だった。そこで、次の問いが生まれた。「どっちの目盛り（赤い色か青い色）を見てはかればいいの？」。「じゃあ、1分間だけ教科書を見てもいいよ」とわたしは伝えた。子どもは納得の表情だった。このように、分度器の測定方法を知る場面でも問いは生まれる。初めてのことだからと教師が丁寧に測定方法を教えることでは、子どもに問いは生まれない。問いと試行錯誤の時間ありきの、納得ではないだろうか。

子どもの問いは、まだ終わらない。わたしは、ある分度器を子どもに渡した。わたしが子どもの頃に使っていたもので、右から始まる目盛りしかない分度器だ。それを手にして先ほどの問題に向き合う子ども。「この分度器じゃあ、アの角度は求められるけど、イの角度は無理やね。だって、115°しか書いてないもん」。そこで、わたしは問い返した。「だったら先生は子どもの頃、どうやって求めたの？」。すると、「そうか。じゃあ、なんとかしたら求めることができるかもしれない」と新たな問いをもった。ここで1時間終了。

2時間目は、前時の子どもの問い「イの角度を先生の赤青なしの分度器を使って、求めることはできないだろうか？」で、開始。この時間の解決方法が実に見事だった。2通りの方法（写真）が出た。1つ目は、180°を基にした考え方。角イ＝180°-115°、よって答え65°。2つ目の考え方には、わたしは驚いた。子どもの言葉をそのまま記す。「90°から115°までは25°あるから、くるりんぱをすればいい」。式は、115-90＝25、90-25＝65。正直、わたしはポカーンとした。その子の考えを図で確かめていくことにして、やっと理解した。90°を基にして、線対称のように角イを移動させたのだった。

子どもの問いの力を痛感した1時間だった。