倍数算を線分図で解く方法
前回は倍数算を比例式で解きましたが、今回は線分図をつかって解く方法を説明します。前回と同じ問題で説明しますので、解きやすい方を身に付けてください。なお、解説には比例式で解く方法も簡単に載せてありますが、詳しくは前回の内容を参照してください。
問題1
太郎君と次郎君の2人の所持金の比は2:1でしたが2人とも50円使ったので,太郎君と次郎君の残金の比は3:1になりました。初めに太郎君が持っていたお金は何円ですか。
(前回の問題1)
解法
倍数算を線分図で解くためには、まず初めと後で変わらないもの(数)を見つけます。この問題では,使った金額は2人とも同じ50円なので,使う前と使った後の2人の所持金の差は変わりません。

例えば太郎君が200円,次郎君が100円持っていた場合,2人の所持金の差は100円です。もし,2人とも80円を使った場合,太郎君の所持金は120円,次郎君は20円となり,2人の所持金の差は100円です。つまり,2人が同じ金額だけ使っても,使う前と使った後とでは所持金の差は変わらないのです。
◆50円を使う前・・・所持金の比は 


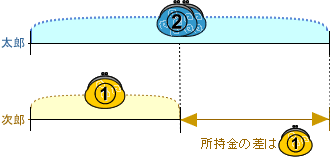
◆50円を使った後・・・所持金の比は 


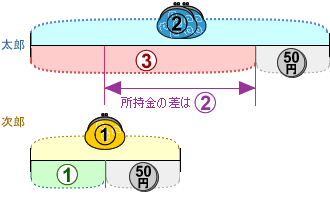
所持金の差は同じはずなのに、比で表すとすると違っています。これではわかりにくいので、所持金の差(比)をそろえて表します。
そろえるときには、差の最小公倍数にそろえることがポイントです。
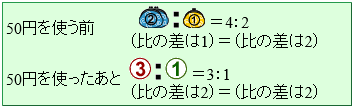

50円を使う前の2人の所持金の差 と使った後の差
と使った後の差 の最小公倍数の2にそろえました。
の最小公倍数の2にそろえました。
そこで、図を次のように書きなおします。
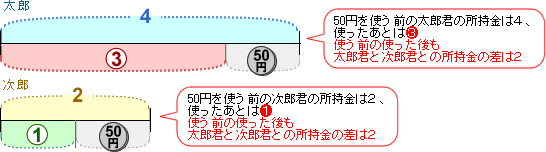

2人の所持金の差を2にそろえたので,この2に対する比がこの図に表されたことになります。つまり,所持金の差を2に決めると,太郎君の最初の所持金は4、50円を使ったあとは3、次郎君の場合は,それぞれ2と1です。少し難しいかもしれませんが,線分図で倍数算を解くときにはこの考え方(2つの線分図の中で共通なもの(比)を決めて他の比を求める)が基本になります。
そして、次の計算ができます。
太郎君の線分図をみると、50円を使う前(4)と使ったあと(3)の差は1で50円に相当しています。
1=50円ならば、4=200円(50×4)、3=150円(50×3)。 つまり、太郎君の最初に持っていた金額4=200円ということになります。
(同じように考えると次郎君が最初に持っていた金額2=100円となります。)
倍数算を線分図で解くときのポイント
まず、初めと後で変わらないもの(数)を見つけ、線分図を書きます。そして変わらないもの(数)の比を最小公倍数でそろえて線分図を書き直して解きます。
この問題を比例式で解く方法はこちら
答え:200円
類題1
花子さんと桃子さんが買い物に行きました。はじめに持っていたお金の比は5:3でした。2人とも同じ400円の品物を買ったので、お金の比は2:1になりました。はじめに花子さんの持っていたお金はいくらですか。
(前回の練習問題)
答え
2000円
問題2
姉と妹の持っているおはじきの数の比は3:2でしたが,姉が妹に7個あげたので,姉と妹の持っているおはじきの数の比は1:3になりました。姉は初めに何個のおはじきを持っていましたか。
(前回の問題2)
解法
この問題でも、初めと後で変わらないもの(数)を見つけます。この問題では、姉が妹におはじきをあげたので、おはじきをあげる前とあげた後とでは、2人のおはじきの合計は変わりません。
この合計をポイントとして考えます
そこで次のような線分図を書きます。
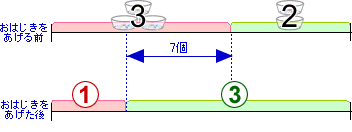
所持金の差は同じはずなのに、比で表すとすると違っています。これではわかりにくいので、所持金の差(比)をそろえて表します。
そろえるときには、差の最小公倍数にそろえることがポイントです。

問題1では、太郎と次郎の所持金の差に着目して比較するため、太郎と 次郎をたてに並べて線分図を書きました。
この問題では、2人の合計に着目して線分図を比較するので、姉と妹を横に並べて書きます。
おはじきをあげる前とあげた後では合計が変わらないはずですが、比にすると あげる前が合計、あげた後が合計4で違ってしまいます。
これではわかりにくいので、比の合計をそろえます。 ここでも、2つの合計の最小公倍数にそろえることがポイントです。


あげる前の合計⑤とあげた後の合計④の最小公倍数の20にそろえます。
合計がそろったので、線分図を次のように書き直します。
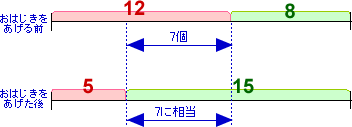
図をみると、あげた7個は比の7に相当しているので、1個は比の1に相当します。
つまり、比の1は1個に相当するので、姉の持っていたおはじき12は12個ということになります。
この問題を比例式で解く方法はこちら
答え:12個
問題3
はじめに水そうAと水そうBの中に入っていた水の量の比は2:3でしたが、Aには水を10リットル入れ、Bからは30リットルくみ出したため、水そうAと水そうBの水の量の比が5:6になりました。はじめに水そうBに入っていた水の量は何?ですか。
(前回の問題3)
解法
この問題では、初めと後でかわらないもの(数)がなさそうです。その場合は、次のように線分図の長さをそろえると解くことができます。ここでは、後の水の量に着目して長さをそろえます。
◆初め・・・水の量の比は②:③
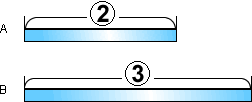
◆後・・・水の量の比5:6
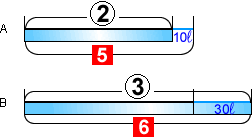
線分の長さを5と6の最小公倍数の30にそろえます(線分全体をAは6倍、Bは5倍します)
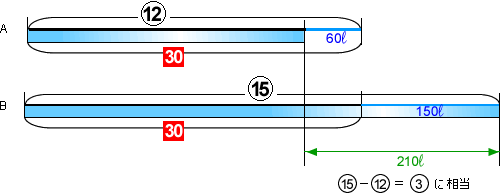
すると、⑮と⑫の差③は210リットル(60リットル+150リットル)にあたるから、①は70リットル(210÷3)にあたることになります。 はじめ、Bに入っていた水は③だったので、210リットル(70リットル×3)になります。
※解説では後の水の量に着目して最小公倍数の30にそろえましたが、はじめの水の量に着目して、2と3の最小公倍数6に線分図そろえても解くことができます。
※この線分図の長さをそろえる解き方は、他の問題でも解けますので、ためしてみてください。
この問題を比例式で解く方法はこちら
答え:210リットル
類題2
「倍数算を比例式で解く方法(基本編)その1」はこちら
答え
96台

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
