学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
倍数算を比例式で解く方法（基本編･その1）
倍数関係（ふつうは比で表される）にある2つの数量が、それぞれ増えたり減ったりした結果、最初とは違う倍数関係（ふつうは比で表される）になるとき、初めの数量や結果の数量を具体的な数量で求める問題を倍数算といいます。倍数算はふつう線分図を使って解きますが、今回は比例式を使って解く方法を紹介します。独特な解き方ですがコツをつかめば、ほとんどの倍数算の問題を簡単に素早く解くことができるからです。このとき方をぜひマスターしてみてください。
問題1
太郎君と次郎君の2人の所持金の比は2：1でしたが2人とも50円使ったので，太郎君と次郎君の残金の比は3：1になりました。初めに太郎君が持っていたお金は何円ですか。
解説
はじめに，太郎君と次郎君の所持金の比は2：1なので、
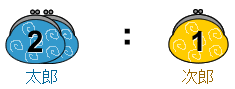
と書きます。（太郎）、（次郎）のように小さくメモしておくとよいでしょう。
この最初の比に○をつけておきます。
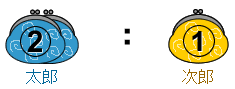
２人とも５０円を使ったので、それぞれの比から50円を引きます。
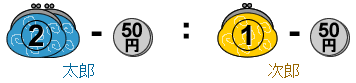
なれるまでは「50円」のように数に単位をつけておくと理解しやすくなります。
その結果、太郎君と次郎君の残金の比は3：1になったので＝３：１とします。
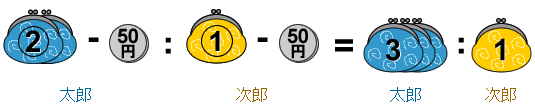
次に外項と内項とをかけ算して＝で結びます。
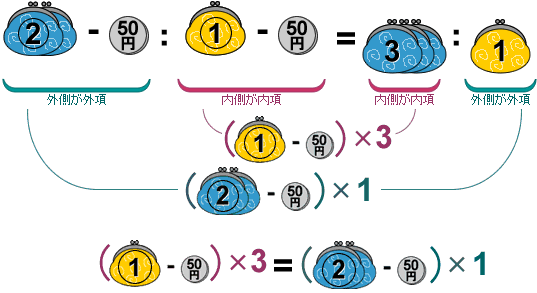
比例式が成り立つとき必ず外項の積(かけたもの)と内項の積(かけたもの)は等しくなります。たとえば，２：３＝10：15という比例式がなりたちますが、 同時に外項の積（２×１５）＝内項の積（３×１０）も成り立っています。
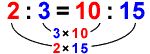
左辺（＝の左）の式は、②と50のそれぞれを1とかけ算します。右辺（＝の右側）は①と50のそれぞれを3とかけ算します。
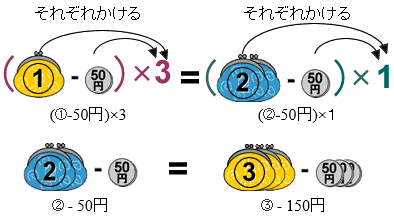
そして、この式を ○＝数 の形にします。結論を先に書くと次のようになります。
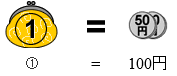
この式の作り方にはルールがあるので、いったん問題の解説を離れて、説明しておきます。
○＝数 にするルール
ちょっとごちゃごちゃしますが、内容は簡単です。
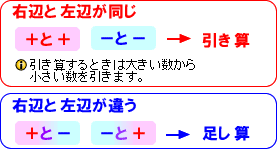
Point1 ○つきの数字の位置に注目
○付きの数字を左側に、ついていない数は右にもってきます
Point2 数の前（左側）の＋と－に注目<
数の前(左側)の＋、－に注目します。なにもついていないときは＋が省略されています。
・・・特に○をつけた数の前には○何もないので＋が省略されています。
Point3 右辺と左辺の＋と－に注目
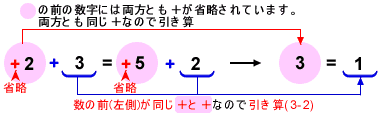
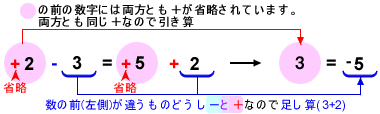
▶例１ ②＋３＝⑤＋２の場合（省略しないで書くと＋②＋３＝＋⑤＋２）
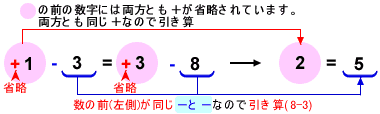
▶例２ ①－３＝③－８ の場合（省略しないで書くと＋①－３＝＋③－８）
▶例３ ④＋３＝⑤－３の場合（省略しないで書くと＋④＋３＝＋⑤－３）
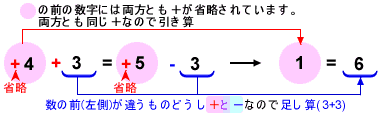
▶例４ ②－３＝⑤＋２の場合（省略しないで書くと＋②－３＝＋⑤＋２）
問題の式にもどります。上のルールにしたがって、○＝数にします。
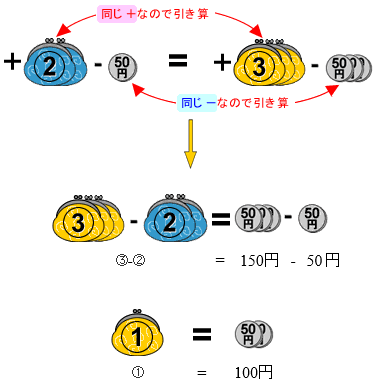
引き算をするときは,単純に大きい数から小さい数を引きます。
この式は何を意味するのでしょうか。
最初に持っていた太郎君と次郎君の所持金の比に○を付けました。
つまり、最初の所持金の比で①は100円に相当するということです。
最初の太郎君と次郎君の2人の所持金の比は②：①でしたので、
太郎君は②に相当する200円（①の2倍）、次郎君は①に相当する100円を持っていたことになります。
検算してみると、2人とも50円を使った場合、太郎君は150円、次郎君は50円残るので比は150：50＝3：1となって問題文とのくいちがいはありません。
答え：200円
問題2
姉と妹の持っているおはじきの数の比は3：2でしたが，姉が妹に7個あげたので，姉と妹の持っているおはじきの数の比は1：3になりました。姉は初めに何個のおはじきを持っていましたか。
解説
はじめに、姉と妹の持っているおはじきの数の比は3：2なので、
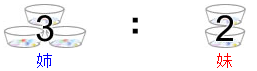
と書きます。次に最初の比に○をつけておきます。
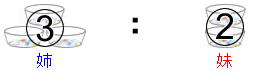
姉が妹に7個あげたので
その結果、姉と妹の持っているおはじきの数の比は1：3になったので、
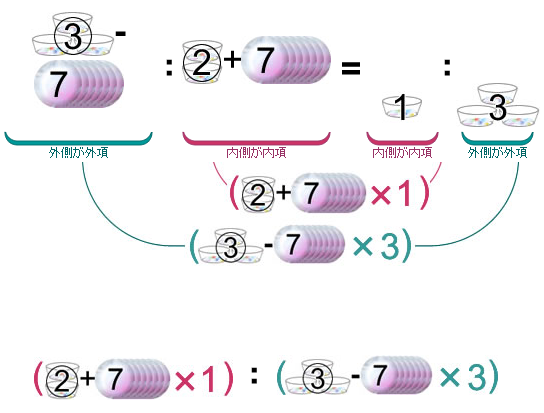
左辺（＝の左）の式は、③と７のそれぞれを3とかけ算をします。右辺（＝の右側）は②と７のそれぞれを１とかけ算をします。
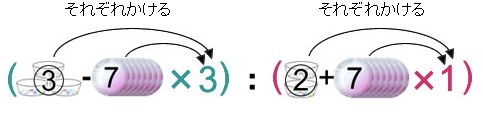
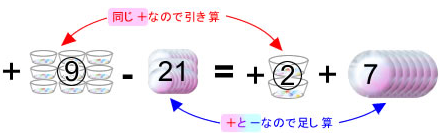
引き算をするときは,単純に大きい数から小さい数を引きます。
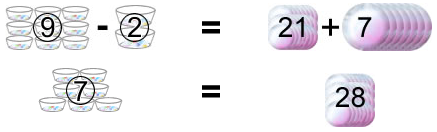
ここで、⑦に相当する数が28なので、①に相当する数は4になります（両方を７でわる）。
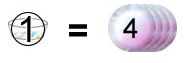
最初に持っていたおはじきの数の比に○をつけました。
すると、最初に姉と妹の持っているおはじきの数の比は③：②だったので
最初に持っていた姉のおはじきの数は③に相当するので（①の3倍）、4×３＝12個
最初に持っていた妹のおはじきの数は①に相当するので（①の2倍）、4×２＝8個
検算してみます。姉が妹に7個あげたので，姉は12－７＝5個残り，妹は7個もらったので，8＋７＝15個になります。
その比は5：15＝1：3となって問題文とのくいちがいはありません。
答え：12個
今日の「倍数算を比例式で解く方法（基本編）」前半はここまでです。後半ではきんたろう先生と一緒に練習問題を解いてみましょう。
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
