倍数算を比例式で解く方法(基本編・その2)
倍数関係(ふつうは比で表される)にある2つの数量が、それぞれ増えたり減ったりした結果、最初とは違う倍数関係(ふつうは比で表される)になるとき、初めの数量や結果の数量を具体的な数量で求める問題を倍数算といいます。倍数算はふつう線分図を使って解きますが、今回は比例式を使って解く方法を紹介します。独特な解き方ですがコツをつかめば、ほとんどの倍数算の問題を簡単に素早く解くことができるからです。このとき方をぜひマスターしてみてください。
問題3
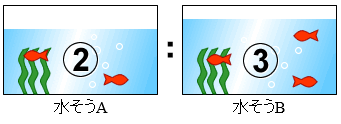
はじめに水そうAと水そうBの中に入っていた水の量の比は2:3でしたが、Aには水を10リットル入れ、Bからは30リットルくみ出したため、水そうAと水そうBの水の量の比が5:6になりました。はじめに水そうBに入っていた水の量は何リットルですか。
解説
はじめに水そうAと水そうBの中に入っていた水の量の比は2:3でした。
Aには水を10リットル入れ、Bからは30リットルくみ出したので、
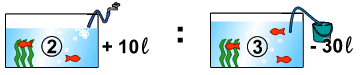
結果として、5:6になったので

そこれまでと同じように計算すると、
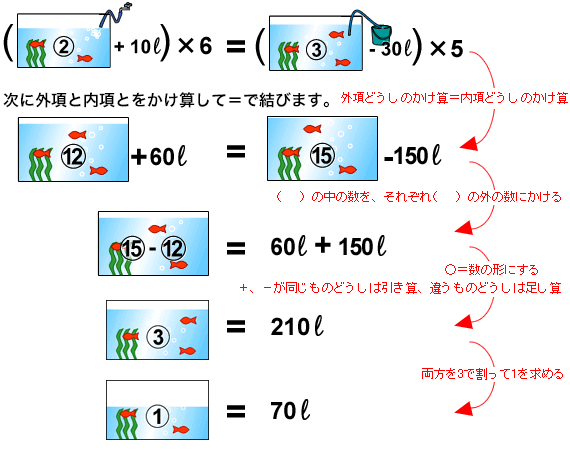

検算してみます。最初Aには140リットル、Bには210リットルの水が入っていたことになりました。比は140:210=2:3で、問題文とのくいちがいはありません。
そして,Aには水を10リットル入れ、Bからは30リットルくみ出したため、Aには150リットル、Bには180リットルの水が残ります。その比は150:180=5:6となってこれも問題文とのくいちがいはありません。
答え:210リットル
問題4
黄色の車と青色の車があり、台数の比は3:5です。青色の車4台を黄色くぬりなおしたところ、台数の比は5:7になりました。車は全部で何台ありますか。
解説
はじめの黄色の車と青色の車の台数の比は3:5でした

青色の車4台を黄色くぬりなおしたので、青色の車は4台減り、黄色の車は4台増えます。

これまでと同じように計算すると、
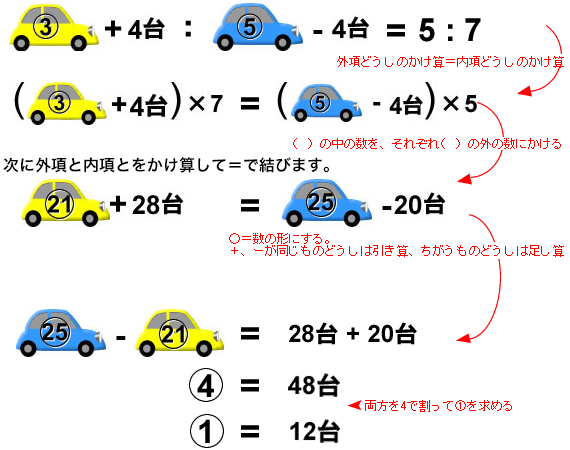
最初は黄色の車と青色の車の台数の比は3:5だったので
黄色の車は③に相当する36台、青色の車は⑤に相当する60台あったことになります。合計96台です

検算してみます。黄色の車は36台、青い車は60台あったことになりました。比は36:60=3:5で、問題文とのくいちがいはありません。そして,青色の車4台を黄色くぬりなおしたので、黄色の車は40台,青い車は56台になります。その比は40:56=5:7となってこれも問題文とのくいちがいはありません。もちろん車の合計は最初も塗り直したあとも合計96台です。
答え:96台
練習問題
花子さんと桃子さんが買い物に行きました。はじめに持っていたお金の比は5:3でした。2人とも同じ400円の品物を買ったので、お金の比は2:1になりました。はじめに花子さんの持っていたお金はいくらですか。
答え
2000円

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
