増やし鬼 鬼になりやすいのは?パート2
「どの場面が一番鬼になりやすいですか?」。児童にとって身近な遊びの場面から、割合の見方を引き出す教材を探してみました。鬼になれる人数が2人で、鬼になりたい人数(希望者)が4人の場面と、鬼の人数が4人で希望者が8人の場面が、鬼のなりやすさが同じだということを、子どもたちは、図を使ったり、実際にじゃんけんをしたりすることで、自分なりの言葉で説明していきました。今日は、1人の児童(Aさん)の考える姿を追っていきながら話を進めたいと思います。
名古屋市立御器所小学校 教諭 松田 翔伍
1/2を示すために図を動かす
Aさんは、4人中2人と8人中4人が同じであることは直観で理解したようでした。ノートには、「4-2=2」という式が書かれていました。まだ言葉では説明できないようでした。
子どもたちは、同じなりやすさを説明するために、「どちらの場面も半分が鬼になれるから、同じなりやすさです」「どちらも1/2です」と発言しました。私は、「半分」や「1/2」という表現に対して、同じ意味をもつ別の表現を考えさせるために、問題場面を表した図を提示しました。
詳しく述べると、まず鬼を決める場面をイメージさせるために、4人の児童を指名し、じゃんけんをさせ、場面を再現させました。そして、その再現を基に赤は鬼の人、白は逃げる人に見立てたカードを、ランダムに貼っていきました。次の場面は、8人でじゃんけんをするため、鬼がなかなか決まりません。すると、「2人1組でじゃんけんすればいいよ。2人でじゃんけんして勝った人が鬼だよ」と助言する声が出ました。そこで、2人1組でじゃんけんをして鬼を決め、カードを貼っていきました。
私は、赤と白のカードを指し示しながら、「どちらの場面も『半分』や『1/2』で同じだと言うのだけれど、これらの図に共通点が見えますか」と問い掛けました。ここから、前回の記事で紹介したような、多様な図が表れます。
Aさんの様子は?
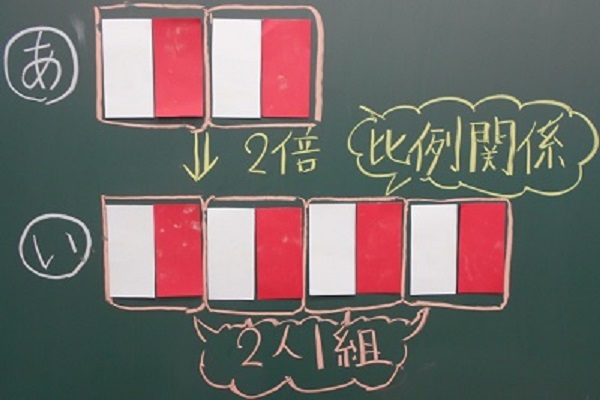
さて、Aさんの様子はどうでしょうか。
Aさんは、右の図を見つめ、「さっき、2人1組でじゃんけんをすればいいと言っていたけれど、2人1組がきれいに作れるね」と、気付くことができました。4人中2人も8人中4人も、2人中1人で分けられるのです。しかし、Aさんはここで問いをもちます。
「みんな、1/2と分数で表しているけれど、どうして1/2で表せるの?」という問いです。
分数で表現できる理由が分からなかったようです。Aさん以外にも、分数による表現でこの場面を表そうとしない子はたくさんいました。その子たちにとって、「1/2」は「2等分したうちの1つ分」です。つまり、何を2等分したのかを明確にしなければ分数と結び付かないのです。
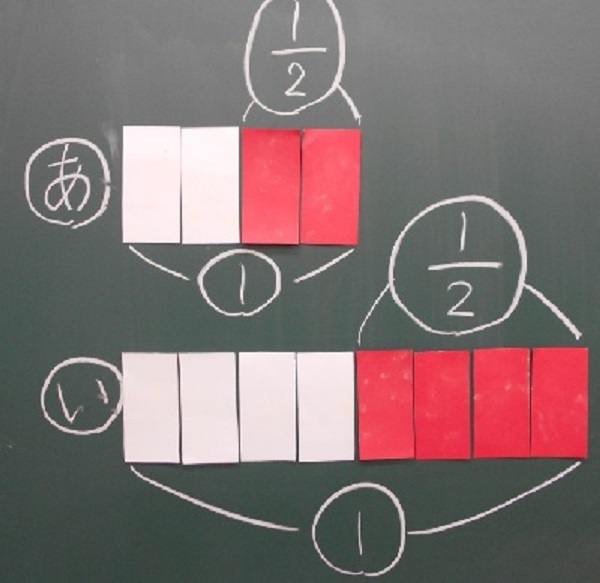
私は、赤と白に分けた図を再度掲示して、「鬼のなりやすさが1/2だとわかりましたが、これは何の1/2ですか」と、問い掛けました。ある子が、「全体の1/2です」と発言しました。しかし、Aさんは納得しません。「1/2」は「2等分したうちの1つ分」なのですから。次に別の子が、「全体を4等分するでしょ。そのうちの2つ分が鬼になれるので、2/4と表せます。約分すると1/2です」と説明しました。また、「全体を1とみると、赤の部分が1/2にあたります」と説明しました。ここでAさんは、「なるほど!!」とつぶやきました。話は逸れますが、割合を表す分数と2等分したうちの1つ分という言葉は、どのように子どもの頭の中で結び付くのでしょうか。調べてみようと思います。
さて、この後、Aさんの「4-2=2」という引き算の考え方について検討していきました。この考え方は、「(鬼の希望者)-(鬼)=(鬼になれない人)」で比べています。鬼になれない人が多い場面では、鬼になりにくくなるのでしょうか。そうではありません。鬼になれない人が多くても、鬼になれる人が多ければ、鬼のなりやすさは高くなります。
差は同じだけど…
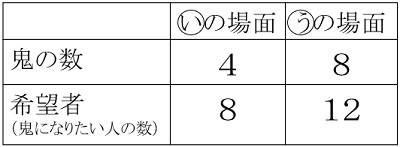
次に、「『い』の場面と『う』の場面が同じだという人もいました。その考え方がわかりますか」と投げ掛けました。ある子が、「『8-4=4』と『12-8=4』をして、鬼になれない数で比べたのだと思います」と発言しました。Aさんは、自分と同じ考え方が取り上げられ、大きくうなずいていました。
すると、別の子たちが、「いつでも使えるのはどっちの考え方かな」「もしも…」と発言しました。これらの言葉は、これまでの授業で児童が発するたびに、短冊で示して強調してきた算数言葉です。多くの子にとって、このように考えることが習慣になってきたことを実感し、うれしい気持ちになりました。
さて、ある子が、「もしも、希望者が10億4人で、鬼が10億人だったら、『10億4―10億=4』で差は4です。8人中4人の時よりも鬼になれる気がします」と発言しました。極端な場合で反例をあげることにより、引き算で比べてはいけないことを説明することができました。
Aさんは、「5-1=4」の式を書き、「5人中1人しか鬼になれない。差が4で同じの『い』の場面よりも鬼になりにくいよ」と、つぶやいていました。差の見方を授業で取り上げることにより、子どもたちは、どんな時に割合の見方をしていくのかを学ぶことができます。Aさんもこの活動によって、納得することができたようでした。
差や割合は、「見えない同じ」だった
今回の授業では、鬼の人数と希望者の人数を設定する際に、割合が同じになる数や、差が同じになる数を取り入れました。異なる質の同じが同時に出てくることで、多くの子が、同じ割合の場面では、鬼のなりやすさが同じであることを直観することができました。今後は、直観したことを、論理的に説明することができるような手だての工夫もしていき、難関単元「割合」を分かりやすくて、考えがいのある授業をしていきたいと思います。
読んでくださり、ありがとうございました。

松田 翔伍(まつだ しょうご)
名古屋市立御器所小学校 教諭
すべての子が考える楽しさを味わえる算数学習を目指し、面白い問題の開発や指導法、子どもとの関わり方について毎日考えています。「できる」「分かる」だけではない、「楽しい」算数授業について私と一緒に考えてみませんか?未来を生きる子どもたちの笑顔のために。
同じテーマの執筆者
ご意見・ご要望、お待ちしています!
この記事に対する皆様のご意見、ご要望をお寄せください。今後の記事制作の参考にさせていただきます。(なお個別・個人的なご質問・ご相談等に関してはお受けいたしかねます。)
この記事に関連するおススメ記事

「教育エッセイ」の最新記事














 アグネスの教育アドバイス
アグネスの教育アドバイス 映画と教育
映画と教育 震災を忘れない
震災を忘れない









 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事 ご意見・ご要望
ご意見・ご要望









