2020.12.24

増やし鬼　鬼になりやすいのは？（パート１）

前回の記事では、「給食じゃんけんにまつわる割合の話」と題して、給食じゃんけんを５年生「割合」の学習の導入で扱うのはどうかと提案しました。子どもにとって身近であること。８人中４人を決めるじゃんけんをすると、２人中１人でじゃんけんしても同じだということに子どもが気付くのではないかということ。この２点がこの教材のポイントでした。しかし、「給食じゃんけん」から、「増やし鬼の鬼のなりやすさ」に場面を変更しました。子どもたちから、割合の見方を引き出すことができたのでしょうか。

名古屋市立御器所小学校　教諭　松田翔伍

増やし鬼にした理由

なぜ、「給食じゃんけん」から「増やし鬼」にしたのか。「給食じゃんけん」だと、余ったおかず（個）に対して、何人（人）にあたるという見方ができます。例えば、おかずが４個余り、８人希望者がいる。この場面だと、１個あたりの希望者２人という見方ができるのです。単位にご注目ください。「個」と「人」です。大きく見れば割合なのですが、これは単元「単位量あたりの大きさ」の学習になります。単元「割合」では、同じ単位の量を扱うのです。これが場面変更の大きな理由です。

図で考えたり、実際にじゃんけんしたり…

どの場面が一番鬼になりやすいですか

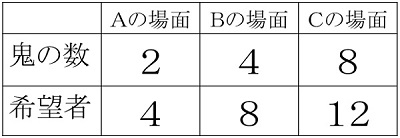
「どの場面が一番鬼になりやすいですか」という問題を出しました。直観で、Ｃの場面が多そうだと多くの子が判断しました。まずは、鬼の数と希望者がそろっていないため、比べにくいということを全体で共有。鬼の数と希望者のどちらかがそろっていれば比べられそうだという見通しをもたせました。

ある子が、「Ａの場面とＢの場面は、どちらも半分が鬼になれます。Ｃの場面は半分以上が鬼になれるから、Ｃが一番鬼になりやすいです」という意見を発表しました。すると、教室中から「Ａの場面とＢの場面は、同じなりやすさです」という声があがりました。

Ａの場面とＢの場面を表した図

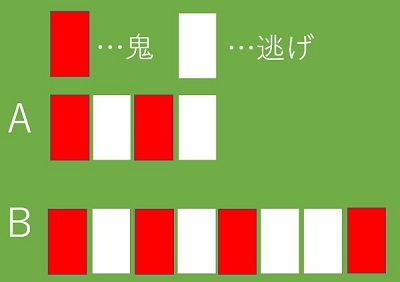
まずは、鬼を決める場面をイメージさせます。Ａの場面を再現するために、４人の子どもを指名して、実際にじゃんけんをさせました。そして、赤色のカードは鬼の人、白色のカードは逃げる人と見立てたカードをランダムに貼り付けていきました。

同様に、Ｂの場面もじゃんけんをしました。次は８人でじゃんけんをするので、なかなか鬼が決まりません。すると、「２人１組でじゃんけんすればいいよ。２人でじゃんけんして勝った人が鬼だよ」と助言する声が出ました。これが後に、確かな理解へとつながる伏線となりました。ここで、「ＡとＢの場面が同じなりやすさなのは、どうしてですか」と全体に投げ掛けて話し合いに入りました。

ある子が、「Ａの場面は、４人中２人鬼になれます。Ｂの場面は８人中４人鬼になれます。どちらも半分が鬼になれるから、同じなりやすさです」と発言しました。続けて、別の子が、「Ａの場面は2/4です。Ｂの場面は4/8です。約分するとどちらも1/2です」と発言しました。やはり、このような場面を与えると、割合を分数で表現する子が多くいました。

半分や1/2。図の中に共通点は見えますか？

子どもが並び替えた図パート１

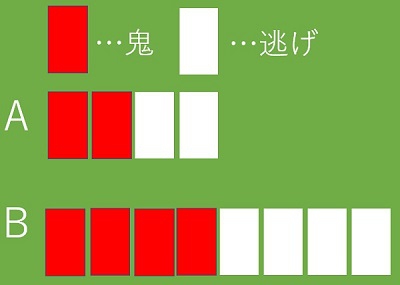
私は、「半分」や「1/2」という表現に対して、図の表現を考えさせるために、「Ａの場面とＢの場面はどちらも半分や1/2と言うのだけれど、これらの図の中に共通点が見えますか」と投げ掛けました。

まず、ある子が、「カードをこのように動かすと1/2が見えるよ」と言って、図パート１のように、赤色のカードと白色のカードを寄せました。

子どもが並び替えた図パート２

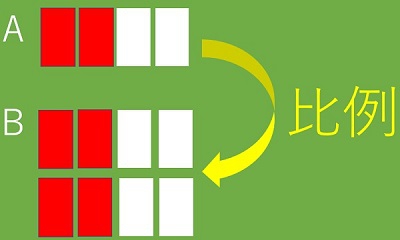
次に別の子が、「Ｂの場面をこのように分けると、同じになります」（図パート２）と言って、図を操作しました。その考え方に対して、ある子が、「Ａの場面の鬼の数と希望者の数をそれぞれ２倍すると、Ｂの場面になります。比例関係が成り立つから、同じなりやすさだと思います」と発言しました。「単位量あたりの大きさの学習でやったね」と話す声が聞こえてきました。前の学習とつなげようとする姿勢がすばらしいですね。

日常の場面とつながった！

子どもが並び替えた図パート３

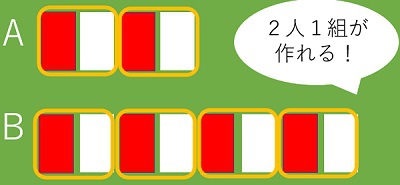
次に別の子が赤と白のカードを交互に置いていきました。そして、「こうすると、どちらも２人１組が作れます」（図パート３）と発言しました。Ｂの場面を再現させた時に出た、「２人１組になればいい」という発言と図が結び付いた瞬間でした。

ここまでで、Ａの場面とＢの場面の鬼のなりやすさは同じだということが、多くの子の納得の上で共有されていきました。

次回へ続く

この後、さらに授業は続いていきますが、ここまでの授業を振り返ってみます。

子どもたちにとって、「半分」や「１／２」という割合を表す表現は分かりやすいようです。４人中２人の場面と、８人中４人の場面が同じ鬼のなりやすさだということは、子どもたちによって納得ポイントが異なるようです。寄せた図（図パート１）を見て納得する子、２人１組が作れる図（図パート３）で納得する子と様々なのです。ですから、多様な図を見せておくことは、子どもたちにとって必要なのですね。

さて、この後、授業では、「１／２は、何の１／２なのか」について解き明かしていくことで、割合の概念化を図っていきました。次回、詳しく書いていきます。

お読みくださり、ありがとうございました。