2020.10.23

楽しさは、どこにある？～子どもの声を軸につくる算数の学び～（②）

算数の楽しさは、どこにあるのでしょうか。人の好みが千差万別のように、その答えは人によって異なります。しかし、分かった瞬間は、誰もがうれしいものです。では、「分かる」とは、一体どのような状態を指すのでしょうか。１つの授業の子どもの様子から、「分かる」について考えてみました。

名古屋市立御器所小学校　教諭　松田翔伍

異分母分数の足し算の学習で…

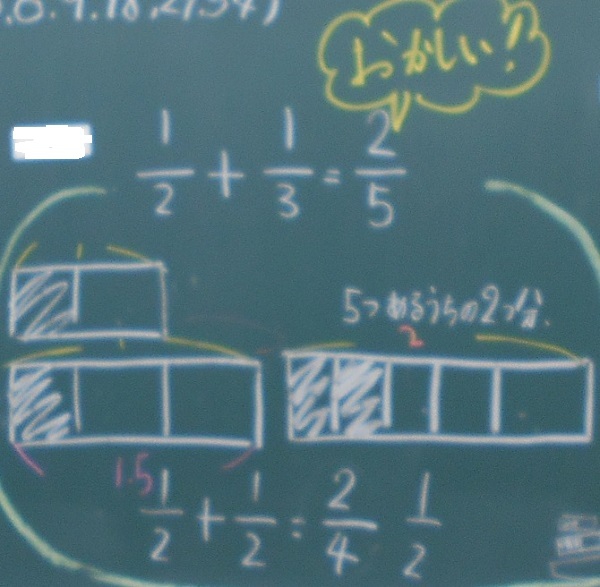
図１　１／２＋１／３＝２／５でもいいのでは？

５年「分数」の学習で、異分母分数の足し算の計算の仕方を考えました。教科書に掲載されている文章題をそのまま扱いました。式は、１／２＋１／３。この計算の仕方を考えるのです。すでに予習を済ませた子たちが、通分をして、３／６＋２／６＝５／６と正答を導き出している中、ある子が右のような図（図１）を書いて、「１／２＋１／３＝２／５でもいいのではないか」と学級に問い掛けてくれました。この子は、通分すると正答が導けることも知っています。しかし、この図のような解釈をすれば、２／５と主張してもよいのではないかと言っているのです。

さて、この考え方をこのように授業で扱ったのは、偶然ではありません。分母同士と分子同士を足すというのは、よくある誤答です。実際、素直に考えれば、このような考え方は出てくるものです。今回は、この考え方を話してくれた子が、このような考えをもっていることを、事前の学習で捉えていたので、この子の発言を促すことができたのです。もしもこの子の誤答がなければ、私の方から投げ掛けていたことでしょう。それほど、価値のある考え方だと思います。

図２　もとにする量をそろえる

さて、これが火種となり、２／５ではおかしいわけをみんなで考えていきました。おかしいことは直観的に分かるようですが、説明となるとじっくり考える時間が必要です。しばらく考える時間をとり、「１／２と２／５を比べて、足したら増えるはずなのに減っていておかしい」という考え方や、「もしも、分母同士と分子同士を足すという考えでよいなら、１／２＋１／２＝２／４（１／２）になっておかしい。いくら足しても１／２のままだなんて！」という考え方で、おかしいわけが説明されました。

その後、「１／２＋１／３＝２／５の世界は、もとにする量がばらばらだからいけない。もとをそろえて考えないといけない」といって、右のような図（図２）が出ました。そして、通分によって分母を６にそろえるという考え方を共有しました。

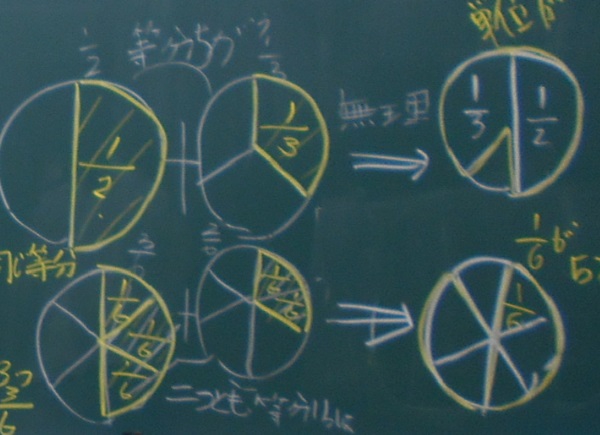
図３　通分前と通分後を比べたピザの図

ここで、「どうして通分すると足し算できるの？」と問い掛けました。そして、「１／２＋１／３と、３／６＋２／６を比べて考えてみよう」と投げ掛けました。

子どもたちは、ピザの図（図３）を書いて、「１／２＋１／３は、パッと見、答えが分からない」、「３／６＋２／６は、パッと見でも分かる」と発言。そこで、「その分かりやすさの違いはどこにあるの？」と問い返しました。すると、「１／２と１／３は、単位がちがう。３／６と２／６は、単位が１／６で同じだ」と言いました。

いつ、分かったのか？

子どもに上のように問い掛け、学習を振り返りました。以下は、子どもから聞いたこの授業の納得ポイントです。

・和は増えるはずという発言で分かりました。
・最初は、２／５だと思っていたけれど、図２を見てよく分かりました。
・図２を見た時に、通分することに気付きました。
この振り返りから分かることは、誤答との対比によって納得することができたということです。正答ばかりではなく、素朴な考え方ではいけないわけを説明できることが、分かった状態の一つの姿と言えるのではないでしょうか。
・図３を比べたら、通分するわけが分かりました。
この子は、問題を出してすぐさま正答を出した子でした。ですが、通分するわけは、この図３を見て納得したようでした。
・〇〇さんのおかげで分かった。
この〇〇さんが、隣の席で相談し合えたことが、この子の納得のきっかけになったようです。
・最初は、２／５と思っていたけれど、通分を使うと聞いて分かった。
この子は、おかしいわけは分かったけれど、正答は分からなかったという子でした。おかしいことが分かることは、ハードルが低いのです。そこから、どのように考えを進めていけるか、我々教師がどのような支援をしていけるか。通分すればよいという見通しをもたせる工夫も必要でした。

「分かる」とは、「よさを味わえていること」

「できる」けれど、「よさが分からない」。この状態が「分かったつもり」という状態ではないでしょうか。「通分すればよいことは分かるけれど、なぜかは分からない」という状態です。この授業では通分すると単位がそろって足し算できるというよさが分かることが大切です。図を見てパッと答えが見える状態にするために、通分したのだと言い換えてもよいかもしれません。子どもたちが、本当に納得できるまで考えることを楽しめるように、今後も考えていきたいと思います。