学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
面積の考え方（第2回）
面積の考え方（第１回）では，三角形や平行四辺形，台形やひし形の面積は，長方形の面積の「たて×よこ」を基本として求めることができることを説明しました。今回は円やおうぎ形の面積です。これらも結局は長方形の面積の「たて×よこ」が基本となります。円やおうぎ形を細かく切って並べ直すと、長方形になるからです。今回も考え方が大切なので，解説形式にしました。
円の面積
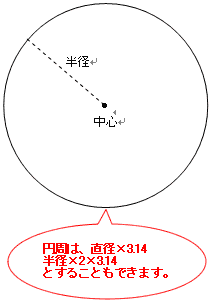
今回は円の面積の求め方を考えてみます。
円の面積は（半径）×（半径）×3.14
ですが、これはどのように導かれるのかを説明します。
前回、図形の一部分を切り取ったり，はりつけたりして面積の求めやすい形（長方形など）に変形して面積を求めました。
面積を変えずに形を変えることを「等積変形」といいます。
円の面積の公式もこの「等積変形」の考え方で導くことができます。
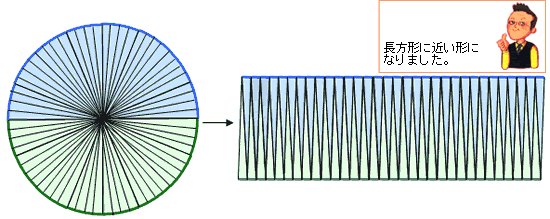
まずは、次のように円を四等分してみます。
そして、四つのおうぎ形を分解して並べてみます。
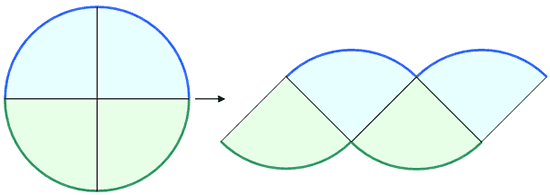
次に円を8等分した場合を考えると次の図のようになります。
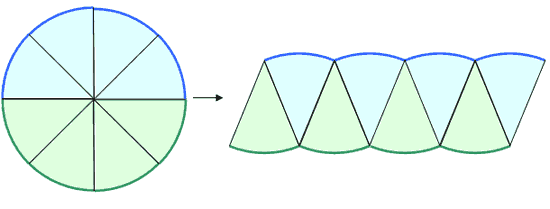
もっと、細かく16等分した場合は次の通りです。
おうぎ形を並べた図が、だんだんと長方形に近づいていくことがわかります。
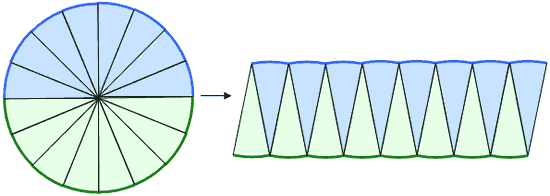
32等分すると次のようになり、かなり長方形に近づいてきました。
もっともっと細かく等分していくと最後には長方形になります。
とりあえずこの図で考えてみます。
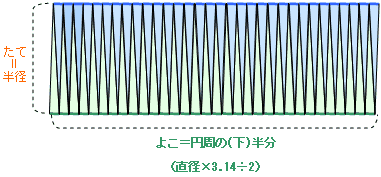
右の図を見ると長方形のたてが半径に相当し長方形のよこ円周の下半分に相当していることがわかります。
長方形の面積は、たて×よこなので、
たて×よこ
=半径×円周の半分
=半径×直径×3.14÷2
=半径× （半径）直径÷2 ×3.14
=半径×半径×3.14
となります。 この長方形は円を細かく等分して、等積変形したものなので、円の面積と同じです。
つまり、円の面積は
半径×半径×3.14
となるのです
おうぎ形の面積
次におうぎ形の面積について考えてみます。
円のときと同じように、小さなおうぎ形に等分割して、並べると次のようになります
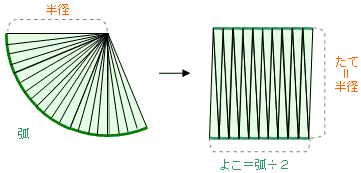
上の図を見ると、たてが半径に相当し、よこは弧の半分の長さに相当していることがわかります。
長方形の面積は、たて×よこなので、
たて×よこ
=半径×弧の半分
=半径×弧÷2
となります。
この長方形はおうぎ形を細かく等分して、等積変形したものなので、扇形の面積と同じです。
つまり、おうぎ形の面積は
半径×弧÷2
となります。
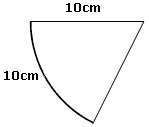
例えば、右の図のように半径10cm,弧の長さ10cmのおうぎ形の面積は
10/(半径) ×10/(弧)÷2＝50cm² となります。
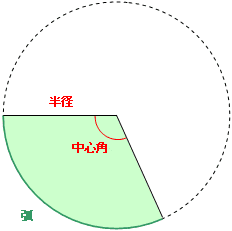
なお、おうぎ形の面積を求めるとき、中心角がわかっている場合は次のように計算できます。
半径×半径×3.14×
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
