面積の考え方(第1回)
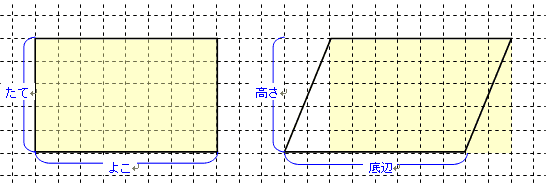
小学校で図形の面積として最初に学習するのは正方形と長方形です。どちらも「たて×よこ」で計算することができます。この正方形や長方形の「たて×よこ」を基礎として,さまざまな図形の面積を求めることができます。三角形や平行四辺形,台形やひし形,円やおうぎ形も結局は「たて×よこ」が基礎となっています。 今回は,問題で正解することよりも,考え方が大切なので,解説形式にしました。
長方形の面積
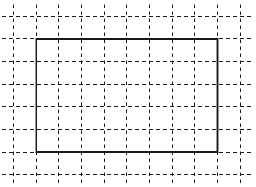
右の図の長方形の面積を求めなさい。(1マスのたて,よこは1cmとします)
長方形の面積は「たての長さ×よこの長さ」だから
5cm×8cm=40cm²
と求めることができます。
なぜでしょうか?
たて1cm,よこ1cmの正方形の面積は1と決められています。
それが40個あるので,40cm²なのです。


もし,1マスのたて,よこが1mとした場合は,この長方形の面積は40m²です。
たて1m,よこ1mの正方形が40個あるからです。
このように,面積はもとになるマス目(正方形)がいくつ分あるかで表します 。
1マスのたて,よこが1mの正方形…1m²
1マスのたて,よこが10mの正方形…10a(=100m²)
1マスのたて,よこが100mの正方形…10ha(=10000m²)
1マスのたて,よこが10kmの正方形…100km²
平行四辺形の面積
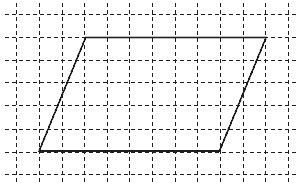
右の図の平行四辺形の面積を求めなさい。(1マスのたて,よこは1cmとします)
面積は基本となるマス目の数で表すことを説明しました。
では,右の図のような平行四辺形の場合はどうでしょうか?
ななめの線があるため,マス目がななめに切られてしまっています。このままでは正しいマス目の数がわかりません。 正しい数を知るには,正方形や長方形で考えなければなりません。
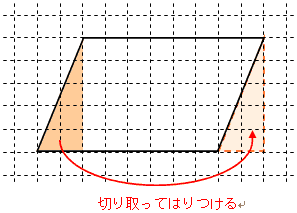
そこで,右の図のように平行四辺形の一部分を切り取って,移動させます。
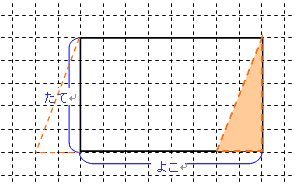
すると右の図のように長方形になるので,正しいマス目の数(面積)がわかります。
マス目の数(面積)は「たて×よこ」なので
5×8=40
マス目1つは1cm²なので,全体の面積は40cm²となります。

このように図形の一部分を切り取ったり,はりつけたりして面積の求めやすい形(長方形など)に変形することは面積を求める上で大きなポイントの1つとなります。基本的な図形だけでなく,複雑に組み合わさっている図形についても応用できます。
面積を変えずに形を変えることを「等積変形」といいます。
結局,平行四辺形の面積は,長方形と同じように,「たて×よこ」で計算できるのです。
ただし,平行四辺形の場合は「たて」のことを「高さ」,「よこ」のことを「底辺」とよぶので,平行四辺形の面積は「高さ×底辺」となります。
平行四辺形の面積=底辺×高さ
(このように公式にした場合,「高さ」よりも「底辺」を先に書くことが習慣になっています)
平行四辺形の面積
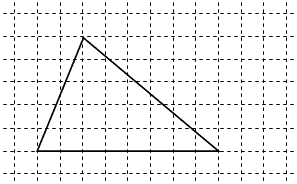
右の図の三角形の面積を求めなさい。(1マスのたて,よこは1cmとします)
次に三角形の場合を考えます。
平行四辺形と同じようにななめの線があるため,マス目がななめに切られてしまっています。
このままではマス目の正しい数(面積)がわかりません。
この三角形の一部分を切り取って,平行四辺形のときと同じように長方形に変形できるでしょうか?
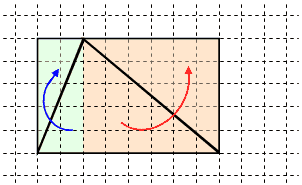
平行四辺形のときほど,簡単ではありませんが,右の図のように,2つの三角形に分けて,同じ三角形(合同な三角形)をそれぞれ上部にくっつけてみます。
すると,長方形になりました。
長方形の面積は,「たて×よこ」なので,
5×8=40cm²
と計算できます。
ところが,この長方形は元の三角形2つ分の面積なので,半分にしなければなりません。
ゆえに,三角形の面積は
40cm2÷2=20cm²
となります。
結局,三角形の面積は,長方形の面積÷2で計算できます。つまり, 三角形の面積=底辺×高さ÷2 となります。

このように合同な図形を,はりつけて面積の求めやすい形に変えることも重要な工夫の1つです。
面積が2倍になるように形を変えることを「倍数変形」といいます。
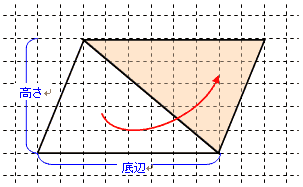
また,右の図のようにして平行四辺形をつくることもできます。
全く同じ三角形(合同な三角形)を右上にくっつけてみます。
すると,平行四辺形になりました。
平行四辺形の面積は,底辺×高さなので,
8×5=40cm²
と計算できます。
ところが,この平行四辺形は元の三角形2つ分の面積なので,半分にしなければなりません。
ゆえに,三角形の面積は
40cm2÷2=20cm²
となります。
結局,三角形の面積は,平行四辺形の面積÷2となります。つまり,
三角形の面積= 底辺×高さ÷2
(平行四辺形の面積)
で,長方形を作った場合と同じ結果になりました。
三角形の面積
右の図の台形の面積を求めなさい。(1マスのたて,よこは1cmとします)
台形の場合はどうでしょうか。
台形もななめの線があり,マス目がななめに切られてしまっています。このままではマス目の正しい数がわかりません。
台形からも同じように長方形や平行四辺形がつくれるのでしょうか?
右の図のように,もとの台形を回転させるような感じで,逆さまにして同じ台形(合同な台形)をくっつけると平行四辺形ができます。
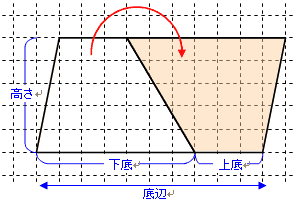
平行四辺形の面積は,底辺×高さなので,
10×5=50cm²
と計算できます。
ところが,この平行四辺形は元の台形2つ分の面積なので,半分にしなければなりません。
ゆえに,台形の面積は
50cm2÷2=25cm²
となります。
結局,台形の面積も,平行四辺形の面積÷2となります。
ただし,右上の図で平行四辺形の底辺に相当するのは,台形の上底+下底なので
台形の面積= (上底+下底)×高さ÷2
(平行四辺形の面積)

今回は,平行四辺形と三角形,台形の面積について説明しましたが,どの図形も長方形の「たて×よこ」が基本となっていることがわかると思います。今回,説明していないひし形の面積についてもぜひ,考えてみてください。次回は円やおうぎ形の面積について説明します。

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
