学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
角度の求め方（第2回） 折り曲げてできる図形の角度
今回は折り曲げてできる図形の角度の求め方を説明します。よく出題される問題です。ポイントは折り曲げることによって作られる合同な図形に着目することです。
今回の解き方のポイント
折り曲げてできる図形の角度･･･折り曲げることによって作られる合同な図形に着目
今回の問題を解くときの基本事項
・三角形の内角の和＝180°
・直線の角＝180°
・三角形の外角と内角の関係
問題1
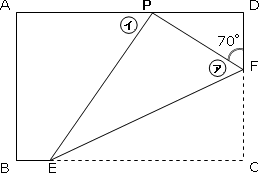
右の図は、長方形ABCDの頂点Cが辺AD上のP点にくるように折り曲げたものです。
このとき、㋐、㋑のそれぞれの角の大きさを求めなさい。
解法
まずは、折り曲げることによってできる合同な図形に着目します。
下の図で水色の直角三角形と黄色の直角三角形が合同です。 合同な図形では対応する角度の大きさが等しいので、下の図のように水色の直角三角形の の角度はと黄色の直角三角形の角ＥＦＣと等しくなります。
このように、合同な図形を見つけて、対応する角をみつけることが、問題を解く第一ステップとなります。
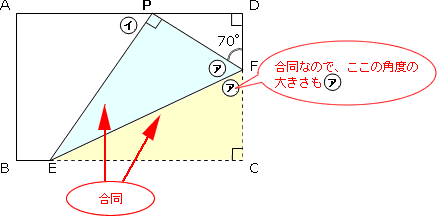
P合同とは回転したり、移動したりするとピタリ！と重ね合わせることができる2つの図形のことです。
（合同な図形は、対応する辺の長さや角度の大きさが全く同じです）
それでは、まずは㋐から求めてみます。
右の図のFに着目すると
直線の角は180°であることより
㋐＋㋐＋70° ＝180°なので、
㋐＋㋐ ＝110°
＝55° となります。
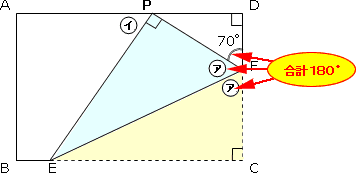
Fに着目すると、直線の角は180°であることより
㋐が２つ分と70°を足すと合計180°なので、㋐2つ分は、180°－70°＝110°です。
よって、㋐1つ分はその半分だから110°÷2＝55°となります。
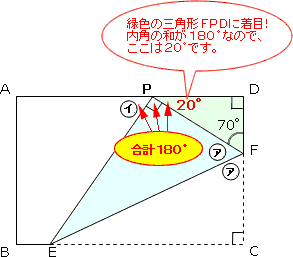
次に㋑を求めてみます。
右の図で三角形FPDに着目すると、三角形の内角の和は180°だから、
180°－（70°＋90°）＝20°
で、角FPDは20°です。
さらにPに着目して、直線の角は180°であることより
㋑＋90°＋20° ＝180°だから
㋑＝70° となります。
この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係（三角の旗）を利用すると簡単に正解が得られる問題はたくさんあります。
Pに着目すると、直線の角は180°であることより
㋑と直角と20°を足すと合計180°です。
よって
㋑は180°－（90°＋20°）＝70° となります。
答え
㋐＝55°、㋑＝70°
問題2
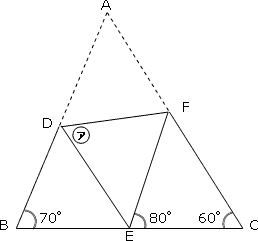
右の図のように、三角形ABCの紙の頂点Aが辺BC上にくるように折りました。
㋐の角の大きさは何度ですか。
解法
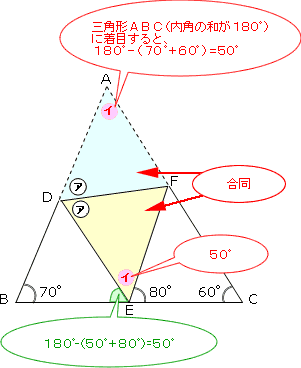
ここでも、折り曲げることによってできる合同な図形に着目します。
右の図で水色の三角形と黄色の三角形が合同です。
右の図で水色の三角形の角㋐
と角
に対応する角を黄色の三角形に記入しました。
は三角形ABCの内角の和が180°であることより次のように計算できます。
＝180°－（70°＋60°）＝50°
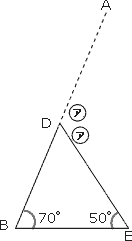
合同の関係より、黄色の三角形のも50°です。
直線の角は180°であることより
角DEB＝180°－（50°＋80°）＝50°
と計算できます。
さらに右の図で、三角形の内角と外角の関係より、
㋐×２＝70°＋50°＝120°
なので、㋐＝60°となります。
（三角形の内角と外角の関係は次の「復習」を参照してください）
答え
㋐＝60°
復習
復習： 三角形の外角と内角
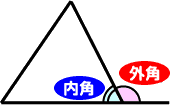
右の図のように三角形の2つの辺でできる角を三角形の「内角」といい、１つの辺を延長して、となりの辺との間につくられる角を三角形の「外角」といいます。
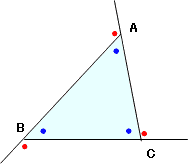
「外角」は三角形の辺の延長の仕方により、違ってきます。例えば、右の図のように延長線を引くと、●が内角、●が外角です。
この内角と外角との間には次の関係があり、とても重要です。
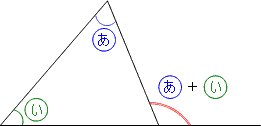
「三角形の１つの外角は、となりあっていない2つの内角の和に等しい」
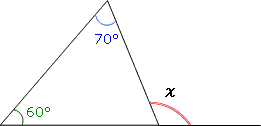
例えば、次の三角形で、χ は70°＋60°で130°になります。
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
