角度の求め方(第1回) 三角形の内角と外角の関係

三角旗とブーメランを見つければ、基本問題はバッチリ!!今回は図形の角度を求め方の説明です。今回ポイントとなるのは「三角形の内角と外角」の関係です。丁寧な説明を心がけた結果,解説中の図がとても多くなってしまいましたが,ゆっくり読んでいただければ,必ず理解できると思います。
重要ポイント:三角形の外角と内角
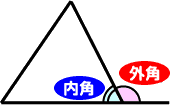
右の図のように三角形の2つの辺でできる角を三角形の「内角」といい、1つの辺を延長して、となりの辺との間につくられる角を三角形の「外角」といいます。
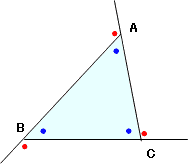
「外角」は三角形の辺の延長の仕方により、違ってきます。例えば、右の図のように延長線を引くと、●が内角、●が外角です。
この内角と外角との間には次の関係があり、とても重要です。
「三角形の1つの外角は、となりあっていない2つの内角の和に等しい」
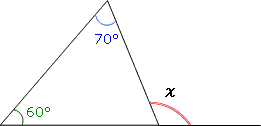
例えば、次の三角形で、χは70°+60°で130°になります。
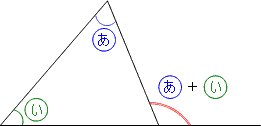
三角の旗を探そう
問題を解くときには、この内角と外角の関係をあてはめることができる場所を図の中にみつけることが、解法のポイントになります。実際には、次のような形を問題の図の中に見つけ出すことになります。三角の旗(はた)を見つけるイメージで考えるとわかりやすいと思います。
問題1
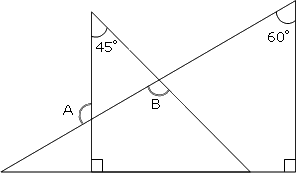
右の図は1組の三角定規を重ねてつくった図形です。角A、角Bの大きさを求めなさい。
解法
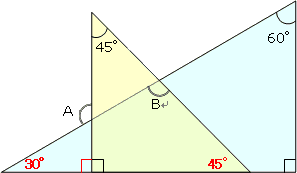
三角定規を組み合わせた問題はとてもよく出題されています。
わかる範囲で角度を図に記入してみましょう(右図の赤文字)。
三角定規では、
「0°・60°・90°」(右図水色)と
「45°・45°・90°」(右図黄色)の
三角形になることが大前提です。
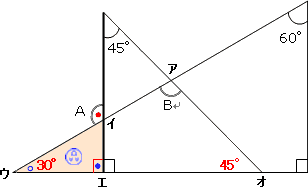
それではまず、角Aからみていきます。
すると角Aは三角形イ、ウ、エの外角になっています。(旗が逆さになっています)
三角形の内角と外角の関係から
●=○+●
角A=30°+90°=120°
と計算できます。
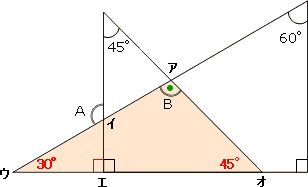
次に角Bはどうでしょうか。
右の図のように角Bは三角形ア、ウ、オの内角の一つになっています。
三角形の内角の和は180°なので、
角B=180°-(30°+45°)
=180°-75°
=105°
と計算できます。
この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係(三角の旗)を利用すると簡単に正解が得られる問題はたくさんあります。
答え
角A=120°、角B=105°
問題2
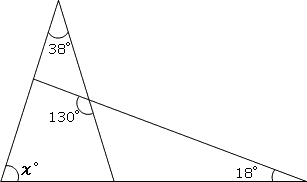
右の図で角χの大きさは何度ですか?
解法
このタイプは三角定規の組み合わせほどではありませんが、よく見かける問題です。有名な形なので「ブーメラン型」と名前が付けられています。この問題も三角形の外角と内角の関係を使うと解くことができます。
まずは、χを求めるために適した三角の旗をみつけてみましょう。いくつかありますが。例えば下の図のように倒れた旗がみつかります。
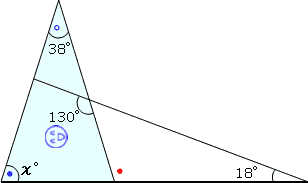
内角と外角の関係から
●+○=●
となるので
χ°+38°=●
・・・ ●がわかればχ°もわかりそうです。
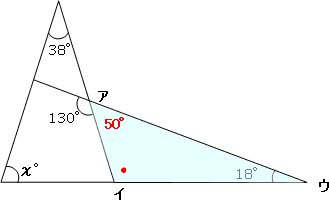
そこで、次の図のように、三角形アイウに注目して考えてみます。
130°の隣の角度は
180°-130°=50°です。
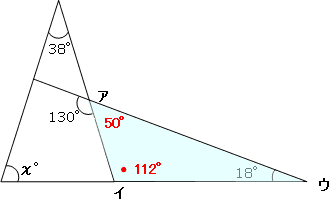
そして、三角形ア、イ、ウの内角の和が180°であることを利用すると、
●=180°-(18°+50°)
=180°-68°
=112°
となります。
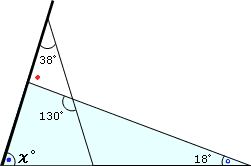
最初の式(内角と外角の関係の式)に戻ると、
χ°+38°=●
だったので、
χ°+38°=112°
χ°=74°
と計算できます。
この他にも右のように、逆さまの旗を見つけて解くこともできます。

ところで、このくぼんだ四角形「ブーメラン型」の問題ですが、もっと簡単に解く方法があります。それは、ブーメラン型特有の次の性質を使います。
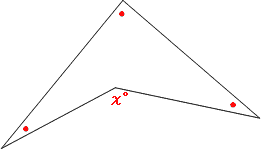
ブーメラン型では、くぼんだ部分の角度の大きさχ°は●で印をつけた角の和と等しくなるのです。(くわしい理由は省略しますが、四角形の内角の和が360°だからです。)
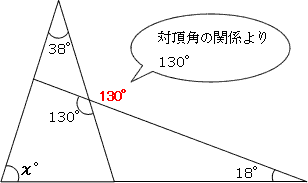
この性質を使って、問題2を考えてみると次のようになります。
χ°と38°と18°の3つをたすと130°に等しくなるので、χ°は74°になります。
(式にすると、χ°+38°+18°=130°)
実は問題1の角Aもこのブーメランの性質を使うと次のように簡単に計算できます。

答え
74°
問題3
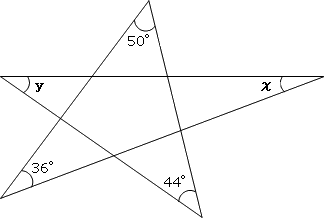
右の図で、角χと角yの大きさの比が3:2のとき、角χとyの大きさはそれぞれ何度ですか。
解法
この問題は角度がわかっている部分が3箇所もあるので、それらをもとに図形に角度を書き込んでいけば、解けそうな問題ですが、ここではまずは、χとyに関係しそうな三角形に着目して、次の図のように外角と内角の関係を利用して解いてみます。
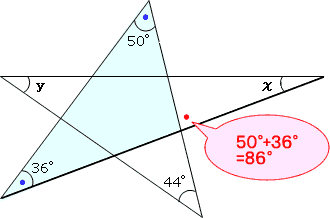
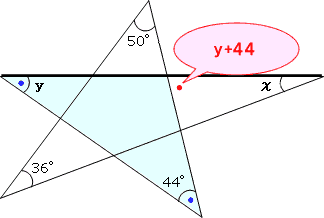
まず右の図のように、外角と内角の関係より
まとめると、次の図のようになります。
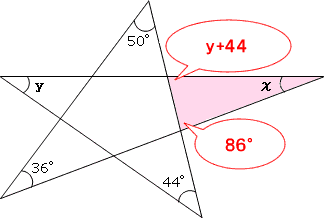
三角形の内角の和は180°だから、次の式がなりたちます。
χ+y+44°+86°=180°
χ+y+130°=180°
χ+y=50°
χ:y=3:2 だからχ=30°、y=20°
問題3でもブーメランを使うと簡単です。

よくみると、旗もあります。三角形の内角と外角の関係より、●+○=● つまり
χ+y=50°
χ:y=3:2 だから
χ=30°、y=20°
と簡単に求めることもできます。
 確かめてみよう!星形のヒミツ
確かめてみよう!星形のヒミツ
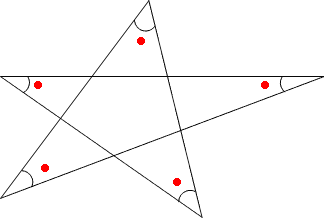
この星型の図形にもヒミツがあります。実は下の図で●をすべてたすと180°になるのです。
この性質を利用すると、この問題3を簡単に解くことができます。説明は省略しますが、ぜひ試してみてください。
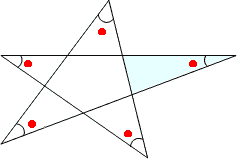
この星型の図形の頂点の角度の和が180°になる理由は、どこか一つの三角形(例えば右図水色の三角形)に着目しての内角と外角の関係を使うと説明できます。詳しいことは省略しますが、ぜひためしてみてください。
答え
χ=30°、y=20°

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
