学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
くふうする計算（第2回）
前回は計算問題の中で，数を組み合わせて10や100をつくって計算しやすくしたり，交換の法則や分配法則などの計算のきまりを利用するなどの工夫をして計算する問題を説明しました。今回は分数の計算を中心に説明します。計算問題はとにかく問題を多く解いて慣れることが大切です。前回と同じようにそれぞれ問題の類題として，昨年度の中学入試問題から練習問題を載せましたので，ぜひチャレンジしてみてください。
問題4
次の計算をしなさい。
（１）15÷20×14÷45×45÷14
（２）1.25÷0.5÷0.125×1 52 ÷3 21
解説
左から順に計算していくと、とても大変そうな問題です。このような計算問題では、整数や小数や分数に直すと計算しやすくなる場合が多くあります。特にこの第4問のように、かけ算とわり算のみの場合は分数に直し、分数のかけ算として計算するとラクにできます。
まず(１)の式を分数に書き直してみます。わり算は逆数のかけ算になることに注意してください。
(1)は次のように、第1位が0になるように数を組み合わせて計算します。
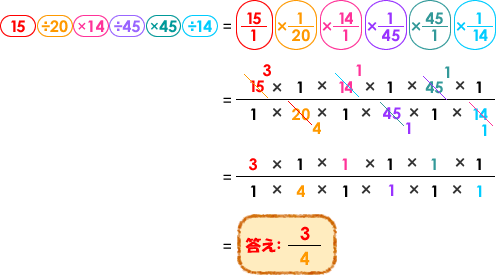
ここでは説明のため、分母分子の1を省略せずに書きましたが、なれてきたら1は書かずに計算してもよいでしょう。
この(2)のように0.5、0.25、0.125に関係する数は計算問題でよくみかけます。これらの小数は分数に直して計算しますが、次のように覚えておくとよいでしょう。
これらを覚えておくと、つぎのようにいろいろな小数を分数に書き直すことができます。
などなど、他にもさまざまな小数を分数に書き直すことができます。
それでは(2)を分数に直して計算してみましょう。
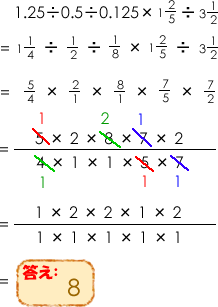
答え：（１） 43 （２）8
練習問題4
次の計算をしなさい。
（１）15×0.25 ÷ 43
〔東京女子学院中学校の入試問題より／2004〕
（2）42÷15÷18÷(56÷45)
〔吉祥女子中学校の入試問題より／2004〕
（３）
〔立教池袋中学校の入試問題より／2004〕
答え
（1）5 （2） 81 （3） 61
問題5
次の計算をしなさい。
（1） 1×21 + 2×31 + 3×41 + 4×51 + 5×61
解説
この問題はとても難しそうですが、結論から先に言うと、実は計算式の最初と最後に着目して
11 - 61 = 66 - 61 = 65
このように簡単に解けてしまいます。
理由は差が１のかけ算が分母にあるとき、次のように分数のひき算と等しくなる性質を利用しています。
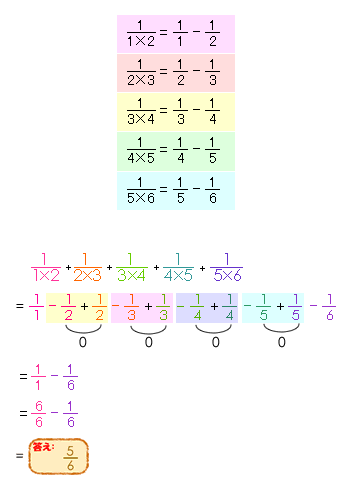
答え：（１） 65
練習問題5
次の計算をしなさい。
（2） 5×61 + 6×71 + 7×81 + 8×91
（自修館中等教育学校の入試問題より／2004）
答え
（2） 454
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
