学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
くふうする計算（第1回）
中学入試の最初の問題は計算問題が定番となっています。この計算問題の中には、基本的な計算のきまりで解くことができる問題もありますが、くふうして解かなければ時間がかかってしまう問題もあります。今回はくふうして解く問題を中心に説明します。 計算問題はとにかく問題を多く解いてなれることが大切です。今回はそれぞれ問題の類題として、昨年度の中学入試問題から練習問題を載せましたので、ぜひチャレンジしてみてください。
問題1
次の計算をしなさい。
（１）53＋14＋96＋17
（２）25×16
（３）3.65－0.745＋2.35－0.255
解説
くふうして計算するための初歩の問題です。どの問題もそのまま左から順に計算していては時間がかかってしまいます。
この問題１のタイプは10や100などかけ算や割り算をするときに計算しやすい数や30や80などのように足し算や引き算をするときに計算しやすい数をつくる工夫が必要です。
(1)は次のように、第1位が0になるように数を組み合わせて計算します。
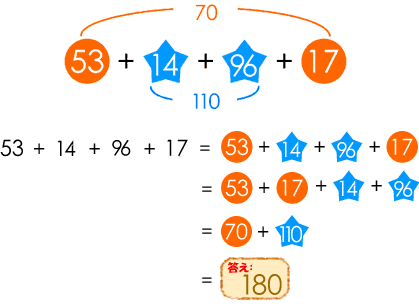
(2)は次のように、かけ算の性質を利用して100をつくります。
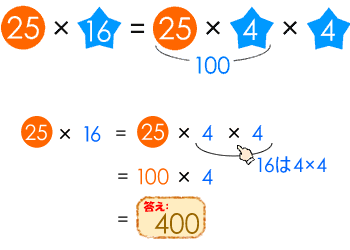
このように工夫すれば、暗算でできてしまうかも知れませんね。
（３）は次のように交換法則を利用するとうまくいきます。
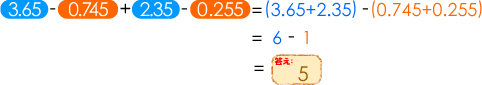
ー（0.745＋0.255）の（ ）内が足し算になっていることに注意してください。
例えば、
10-3-5 =7-5
=2
のように計算ができますが、ここでは
10-(3+5) =10-8
=2
という考え方で計算します。
(３)の問題はこの方が効率的だからです。
つまり、２つの数を引くということは、２つの数を足したものを引くことと同じです。
答え：（１）180 （２）400 （３）5
練習問題1
次の計算をしなさい。
298－179－61＋102
（横浜英和女子学院中学校の入試問題より／2004）
答え
160
問題2
次の計算をしなさい。
（１）10＋20＋30＋40＋50＋60＋70＋80＋90
（２）101＋103＋105＋107＋109＋111
解説
規則的に連続した数の足し算です。この問題も左から順に足し算していては時間がかかってしまいます。
（１）は次のように左右両サイドから順に組み合わせて足していくと、同じ数（100）をいくつかつくることができます。
このように、100が４つ、50が１つできたので、合計は450となります。
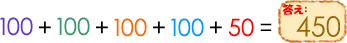
他にも次のような考え方ができます。まず、規則的に連続した数の和（合計）の平均は真ん中の数になります。ここでは50です。
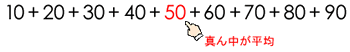
合計は平均×個数なので、50×9＝450として計算することができます。
（２）も（１）と同じ方法で解くと次のようになります。
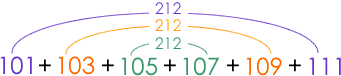
つまり、212×3＝636が正解です。
また、次のような工夫もできます。
10の位の数まで注目して、すべて足します。
1＋3＋5＋7＋9＋11＝36
100×6＝600
合計は
36＋600＝636
この問題も平均の考え方で解くことができます。
まず、規則的に連続した数の和（合計）の平均は真ん中の数になります。
ここでは、個数が6個で偶数なのでちょうど真ん中の数はありません。このような場合は、105と107の真ん中の106が平均になります。
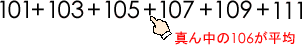
合計は平均×個数なので、106×6＝636として計算することができます。
※この第2問では、平均の考え方での解き方も説明しましたが、これは規則的に連続する数の中で、一定の数が足されることによって増えていく連続した数の列（等差数列）のみで通用するものです。
例えば、2＋4＋8＋16＋32＋64のような一定の数がかけられることによって増えていく数の列（等比数列）にはあてはまりません。
答え：(1)450 (2)636
練習問題2
次の計算をしなさい。
1.1＋2.2＋3.3＋4.4＋5.5＋6.6＋7.7＋8.8＋9.9
（日本大学豊山中学校の入試問題より／2004）
答え
49.5
問題3
次の計算をしなさい。
（１）2.5×12＋2.5×88
（２）6.51×3.14＋3.17×3.14－4.68×3.14
（３）31.5×2×3.14＋18.5×2×3.14
解説
ここでは、共通な数がある場合は、分配の法則を利用して計算します。
（１）は2.5が共通な数です。次のように分配の法則を利用します。
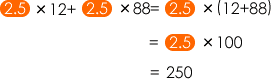
２）は3.14が共通な数です。
(２)は少々計算が大変ですが、工夫なしで左から順に計算しているよりははるかに効率的です。
このようにかけ算されている数が＋や－で結ばれている計算で、共通な数があるときは、共通でない数の部分を計算して、共通な数にかければ答えが出てきます。
3×●＋4×●－2×●＝(3＋4－2)×●
少々慣れが必要かもしれませんが、入試問題でもよく出題されるパターンなので、しっかり練習してください。
（３）は、2×3.14を共通の数として考えるとうまくいきます。
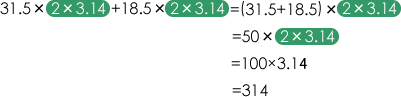
ここのように複雑に見える問題でも、工夫をすると10や100などの計算しやすい整数が自然と出てきて、計算が簡単になる場合が入試問題では多く見られます。
答え：(1)250 (2)15.7 (3)314
練習問題3
次の計算をしなさい。
（１）3.8×7.2＋6.2×7.2
（お茶の水女子大学付属中学校の入試問題より／2004）
（２）0.23×24＋1.35×24＋24×2.42
（桜美林中学校の入試問題より／2004）
答え
(1)72 (2)96
トピック
「1から100までの数（整数）全部たすといくつになりますか？」これは、数学者のガウスが少年のころ先生から出されて、あっという間に解いてしまい。みんなを驚かせたそうです。この問題をガウス少年は次のように解きました。
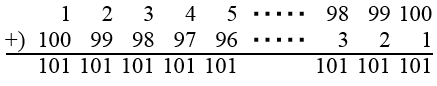
すると、すべて101にきれいにそろいました。101が100個できたので、101を100回たすと、
101×100=10100
になります。これは、1から100までの数を2回足したものなので、半分にして
10100÷2=5050
が正解です。
ガウス少年は一見大変そうに見える足し算を工夫して簡単に計算したわけです。このガウス少年の方法で今回の問題２を解くことができます。逆に問題２で解説した方法でこの問題を計算することもできます。どちらもぜひ試してみてください。
（「くふうする計算」次回へ続く）
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
