約数・公約数・最大公約数（第3回） この単元の最終回

前回の復習で、「47をわると5あまる整数」をすべて求めてみましょう。
解法を見る


60、78、105の3つの数を□でわったら、あまりはすべて同じになりました。□にあてはまる数を求めなさい。
解法を見る


かき89個、りんご123個、みかん140個を同じ数ずつ何人かの子どもに分けると、どのくだものも同じ数だけあまりました。こどもの人数を求めなさい。
解法を見る


Aを55、Bを76、 Cを114とします。この3つの整数を、それぞれある整数でわると、AとBはあまりが等しくなり、Cのあまりは、Aのあまりより4だけ小さくなります。ある整数はいくつですか。
解法を見る

---

　前回の復習で、「47をわると5あまる整数」をすべて求めてみましょう。

■ 解法
　「47をわると5あまる」ということは、5だけ多かったということですから、47から5をひいた42をわればわり切れるということです。それゆえ、この問題を解くためには、まず、42の約数を求めることでした。
　ここで大切なことは　　ポイント：わられる数からあまりを引けば、わりきれる　ということです。

図にすると次のようになります。


47＝5(あまり)＋42(あまりをひいた数)として考え、42をわりきる数つまり42の約数を求めればよいのです。

42の約数1、2、3、6、7、14、21、42のうち、5よりも大きい数は6、7、14、21、42 で、これが正解です。1、2、3が正解でない理由は前回の「準備体操」を参照してください。

　
■ 答え：6、7、14、21、42

---

60、78、105の3つの数を□でわったら、あまりはすべて同じになりました。□にあてはまる数を求めなさい。

■ 解法
この問題の正解は、わられる数のそれぞれの差（18、27、45）の公約数になります。正解を求めることは、簡単ですが、なぜ、約数の知識が使えるのかを、図で説明します。少し複雑だと思いますが、よく図を見て考えてください。
まずは、60と78で考えてみます。



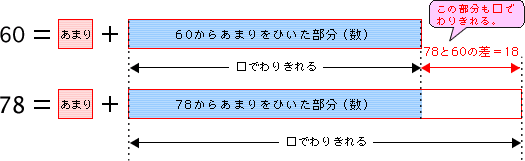
この図は60と78をあまりとわりきれる部分に分けて、図にしたものです。
60からあまりをひいた部分（数）は、□でわりきれます（ポイント参照）。
78からあまりをひいた部分（数）も、□でわりきれます（ポイント参照）。
では、78と60の差＝18の部分はどうでしょうか？
やはり、□でわりきれるはずです。
78と60の差の部分はあまりを含めて78から60をひいた数だからです。

このことをくわしく説明すると、まず、上の「78＝」の図で、78からあまりをひいた部分（数）は、□でわりきれます（ポイント参照）。水色の部分も60からあまりを引いた部分に等しいので、□でわりきれます。そのため、78と60の差の部分も□でわりきれなくてはならないのです。

ここまでの説明でわからない人は次の具体例を見てください。

具体例）9と13を2でわったとき（どちらもあまりは1）

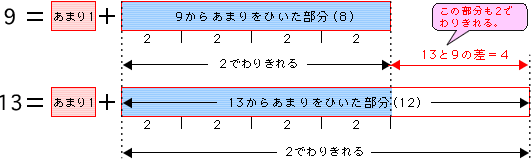説明を続けます。78と60の差である18が□でわりきれるということは、□は18の約数であることがわかります。
つまり□の候補としては、1、2、3、6、9、18があげられます。
ところが、この問題は、105を□でわっても60や78をわったときと同じあまりになるということですので、先の図で同じように考えると、
　・105と60の差である45も□でわりきれる。
　・105と78の差である27も□でわりきれる。
まとめると、□は18（60と78の差）をわっても、45（105と60の差）をわっても、27（105と78の差）をわっても、とにかく3つの数どれをわっても□で割り切れなければならないことになります。
いいかえると、□は18、45、27の公約数ということになります。


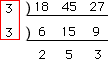
18、45、27の最大公約数は9です。最大公約数の約数が公約数なので、
18、45、27の公約数は、1、3、9です。
ところが、1と3は3つの数をわりきってしまうので（あまりがないので）正解ではありません。9が正解です。

実際にわり算をしてみると、
60÷9＝6・・・6
78÷9＝8・・・6
105÷9＝11・・・6
すべて同じあまり6になります。


■ 答え：9

---

かき89個、りんご123個、みかん140個を同じ数ずつ何人かの子どもに分けると、どのくだものも同じ数だけあまりました。こどもの人数を求めなさい。

■ 解法
この問題は問題1と同じタイプで、
「89、123、140の3つの数を□でわったら、あまりはすべて同じになりました。□にあてはまる数を求めなさい。」と言いかえることができます。
　□がこどもの人数になります。
　問題1と同じように、まず89、123、140の3つの数の差を求めます。

123－89＝34
140－123＝17
140－89＝51



つぎに、これら3つの数の最大公約数を求めると、17となります。
17の約数は1と17ですが、1でわっても（1人に分けても）、あまりは0なので、1は正解ではありません。よって17（17人）が正解です。

実際にわり算をしてみると、
89÷17＝5・・・4
123÷17＝7・・・4
140÷17＝8・・・4
すべて同じあまり4になります。

つまり、17人のこどもに平等に分けたら、かきもりんごもみかんも4個ずつあまることになります。


■ 答え：17人

---

Aを55、Bを76、 Cを114とします。この3つの整数を、それぞれある整数でわると、AとBはあまりが等しくなり、Cのあまりは、Aのあまりより4だけ小さくなります。ある整数はいくつですか。

■ 解法
この問題では、Cのあまりだけ4小さいので、これまでと違って、あまりがすべて同じではありません。そこで、CのあまりもAやBと同じにすれば、これまでの問題と同じように解くことができます。
CのあまりがAやBよりも4小さかったわけですから、Cよりも４大きい、118であれば、あまりが同じになるはずです。
よって、この問題は「55、76、118の3つの数を□でわったら、あまりはすべて同じになりました。□にあてはまる数を求めなさい。」と言いかえることができます。
これまでと同じように、まず55、76、118の3つの数の差を求めます。

76－55＝21
118－76＝42
118－55＝63

つぎに、これら3つの数の最大公約数を求めると、 21となります。


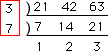
21の約数は1、3、7、21ですが、このうち問題文の条件にあてはまるものは、7と21です。


■ 答え：7または21

実際にわり算をしてみると

55÷1＝55・・・0 76÷1＝76・・・0 114÷1＝114・・・0

不適合

55÷3＝18・・・1 76÷3＝25・・・1 114÷3＝38・・・0

不適合

55÷7＝7・・・6 76÷7＝10・・・6 114÷7＝16・・・2

正解

55÷21＝2・・・13 76÷21＝3・・・13 114÷21＝5・・・9

正解