約数・公約数・最大公約数（第2回） わり算のあまりの問題

47をわると5あまる整数をすべて求めなさい。
解法を見る


56と80のどちらをわっても8あまる整数をすべて求めなさい。
解法を見る


100をわると4余り、72をわると8あまる整数をすべて求めなさい。。
解法を見る


26をわると2あまり、55をわると7あまり、35をわると3あまる整数を求めなさい。
解法を見る

---

47をわると5あまる整数をすべて求めなさい。

■ 解法
「47をわると5あまる」ということは、5だけ多かったということですから、47から5をひいた42をわればわり切れるということです。
42をわり切る整数は、42の約数です。前回説明した方法で約数を求めてみます。

〔42の約数〕

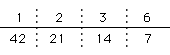
42の約数は、1、2、3、6、7、14、21、42の合計8つになります。
これら8つの数はすべて42をわり切ることができます。
これら8つの数で47を実際にわってみると、次のようになります。



この結果をみると、たとえ42の約数でも1、2、3でわってもあまりが5になりません。6以上でわれば、あまりが5になります。あまりが5なるためには、わる数はあまりの5より大きい数でなければならないのです。わからない人は次の例の図で考えてみましょう。

例1）　47÷7の場合（6あまり5）



例2）　47÷3の場合（15あまり2）


この例2を、3が14個＋【3が1個、2が1個】と考えると、とりあえず、あまりが【5】となりますが、このあまりの5の中に割る数の3がもうひとつ入ることができるのです。
47÷3＝14・・・5（あまり５）と考えることもできますが、算数では、このようなルールはありませんので、
47÷3＝15・・・2（あまり2）としなければならないのです。

ここまでを、ふりかえってみると、「47をわると5あまる整数」を求めるためには、「42の約数」を求め、その中で、わる数の5よりも大きい整数が正解になります。
42の約数1、2、3、6、7、14、21、42のうち、5よりも大きい数は6、7、14、21、42
で、これが正解です。


■ 答え：6、7、14、21、42

---

56と80のどちらをわっても8あまる整数をすべて求めなさい。

■ 解法
この問題1を解くためには、48と72の公約数のうち、8より大きい数を求めれば正解です。その理由を説明します。
まず、56をわると8あまる数を考えてみましょう。
56をわると8あまるということは、8だけ多かったということですから、56から8をひいた48であれば割り切れるはずです。すると、48をわりきる数は48の約数なので、
1、2、3、4、6、8、12、16、24、48の10個です。

〔48の約数〕

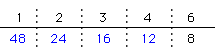
ただし、準備体操で説明したように、わる数はあまりの8より大きい数でなければなりません。
よって、56をわると8あまる数は　　12、16、24、48　　です。

次に、80をわると8あまる数を考えてみましょう。
80をわると8あまるということは、8だけ多かったということですから、80から8をひいた72であれば割り切れるということです。すると、72をわりきる数は72の約数なので、
1、2、3、4、6、8、9、12、18、24、36、72の12個です。

〔72の約数〕

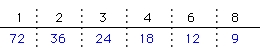
これも、わる数はあまりの8より大きい数でなければなりません。
よって、80をわると8あまる数は　　9、12、18、24、36、72　　です。

ここまでをまとめてみます。
56をわると8あまる数・・・12、16、24、48（48の約数のうち8より大きい数）
80をわると8あまる数・・・9、12、18、24、36、72（72の約数のうち8より大きい数）

問題で求めていることは、56と80のどちらをわっても8余る整数なので、両者を比べて共通なものを見つければよいわけです。例えば、9は80をわると8あまりますが、56をわってもあまりは8ではありません。ところが、12は56をわっても80をわっても8あまりますから、12は正解のひとつです。同じように考えていくと16、18はダメで、24も正解です。残りの36、48、72はだめです。


■ 答え：12と24

結局、この問題を解くためには、48と72の公約数を求めればいいことになります。ただし、準備体操で説明したように、わる数はあまりより大きくなければならないので、8よりも大きな数でなければなりません。
この問題をいいかえると「48と72の公約数のうち、8より大きい数を求めよ」ということになります。

〔別の考え方〕
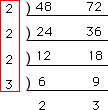48と72の最大公約数は、2×2×2×3＝24
最大公約数の約数が公約数なので、48と72の公約数は、
24の約数になるので、
1、2、3、4、6、8、12、24
この24の約数のうち、8より大きい数は、12と24（正解）

---

100をわると4余り、72をわると8あまる整数をすべて求めなさい。

■ 解法
同じように考えてみましょう。100をわる場合と72をわる場合で分けて考えます。

100をわる場合
100をわると4あまるということは、100から4をひいた96であれば割り切れるということです。ただし、準備体操で説明したように、わる数はあまりの4より大きい数でなければなりません。96をわりきることのできる数は96の約数なので、

〔96の約数〕

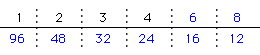
72をわる場合
同じように、72をわると8余るということは、8だけ多かったということですから、72から8をひいた64であれば割り切れるということです。ただし、準備体操で説明したように、わる数はあまりの8より大きい数でなければなりません。

〔64の約数〕

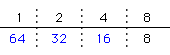
ここまでをまとめてみると
100をわると4あまる数・・・6、8、12、16、24、32、48、96
（96の約数のうち4より大きい数）

72をわると8あまる数・・・16、32、64
（64の約数のうち8より大きい数）

100をわると4余り，72をわると8あまる整数を求めるためには，96と64の公約数をのうち，8より大きいもの（細かく言うと4よりも8よりも大きい数）を求めればよいので，16と32が正解です。

■ 答え：16と32

結局、この問題を解くためには、96と64の公約数を求めればいいことになります。ただし、準備体操で説明したように、わる数はあまりより大きくなければならないので、８よりも大きな数でなければなりません。
この問題をいいかえると「96と64の公約数のうち、8より大きい数を求めよ」ということになります。

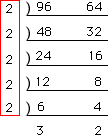
〔別の考え方〕 96と64の最大公約数は、2×2×2×2×2＝32 最大公約数の約数が公約数なので、96と64の公約数は、 32の約数になるので、 1、2、4、8、16、32 この32の約数のうち、8より大きい数は16と32（正解）

---

26をわると2あまり、55をわると7あまり、35をわると3あまる整数を求めなさい。

■ 解法
これも、いままでと同様に考えると、24と48と32の公約数のうち7より大きい数を求めればよいことになります。

〔24の約数〕

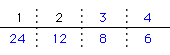
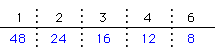
〔48の約数〕

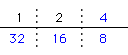
〔32の約数〕

26をわると2あまる数・・・3、4、6、8、12、24（24の約数のうち2より大きい数）
55をわると7あまる数・・・8、12、16、24、48（48の約数のうち7より大きい数）
35をわると3あまる数・・・4、8、16、32（32の約数のうち3より大きい数）

これらに共通な数は8でこれが正解。


■ 答え：8

結局、この問題を解くためには、24と48と32の公約数を求めればいいことになります。ただし、準備体操で説明したように、わる数はあまりより大きくなければならないので、７よりも大きな数でなければなりません。
この問題をいいかえると「24と48と32の公約数のうち、7より大きい数を求めよ」ということになります。

〔別の考え方〕
24と48と32の最大公約数は、2×2×2＝8
最大公約数の約数が公約数なので24と48と32の公約数は、
8の約数になるので、
1、2、4、8
この8の約数のうち、7より大きい数は8（正解）