約数・公約数・最大公約数（第1回）

（1）30と45のそれぞれの約数と公約数、最大公約数を求めよ。
（2）28と42のそれぞれの約数と公約数、最大公約数を求めよ。
解法を見る


たてが30cm、よこが45cmの長方形の紙があります。この紙から同じ大きさの正方形を紙が余らないようにに切り取ります。正方形をできるだけ大きくするには、1辺を何cmにすればよいでしょうか。また、このとき何枚の正方形を切り取ることができますか。
解法を見る



りんご28個とみかん42個の両方を、できるだけ多くの子供に平等に分けます。余りがないように分けると、何人の子供に分けることができますか。
解法を見る

---

（1）30と45のそれぞれの約数と公約数、最大公約数を求めよ。
（2）28と42のそれぞれの約数と公約数、最大公約数を求めよ。

■ 解法
まずは、約数・公約数・最大公約数の意味を覚えましょう。次の文の意味がよくわからない場合は、この問題1を解きながら、理解しましょう。

・「約数」…ある整数をわり切ることができる整数をある数の約数といいます。
・「公約数」…2つ以上の整数の共通な約数を、それらの整数の公約数といいます。
・「最大公約数」…公約数の中で、最も大きい約数を最大公約数といいます。

ある整数をわり切ることができる整数をある数の約数といいます。例えば、6の約数は1、2、3、6の4つで、どの数も6をわり切ることができます。
同じように考えると、30の約数は、1、2、3、5、6、10、15、30の8つです。どの数も30をわり切ることができます。
基本的に数が大きくなるほどその数の約数は増えていきますが、もれなく見つけることができるかどうか、ちょっと心配ですね。そこで、約数には必ずペアとなる相手がいるという性質を利用して、次のように2つ1組で求めていくと速く、より正確に求めることができます。


■30の約数の求め方（かけて30になる組み合わせを1×30から順に求めていく）

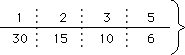上の数と下の数をかけると 30になる

■45の約数の求め方（かけて45になる組み合わせを1×45から順に求めていく）

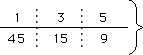上の数と下の数をかけると45になる

よって、30の約数は、1、2、3、5、6、10、15、30
45の約数は、1、3、5、9、15、45

公約数は、共通の約数だから、1、3、5、15となります。
最大公約数は、公約数の中で最も大きい約数だから15です。

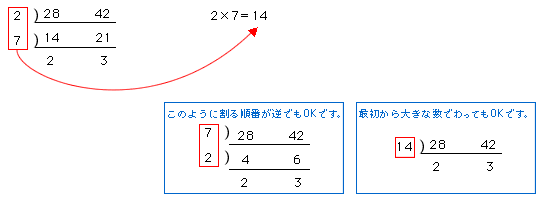
最大公約数を求めるもう一つの方法に連除法という方法があります。どちらでもわることのできる数（1以外）を見つけて、次々に割っていく方法です。

連除法による最大公約数の求め方

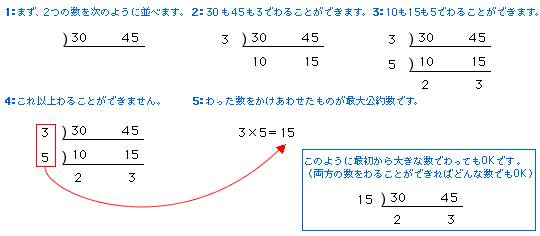
同じように（2）も解いてみましょう。

■28の約数（かけて28になる組み合わせを1×28から順に求めていく）

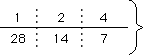上の数と下の数をかけると28になる。


■42の約数（かけて42になる組み合わせを1×42から順に求めていく）

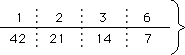上の数と下の数をかけると28になる。

よって、28の約数は1、2、4、7、14、28
42の約数は1、2、3、6、7、14、21、42

公約数は、共通の約数だから、1、2、7、14となります。
最大公約数は、公約数の中で最も大きい約数だから14です。

連除法では

■ 答え：
（1）30の約数　1、2、3、5、6、10、15、30
45の約数 　1、3、5、9、15、 45
公約数　1、3、5、15
最大公約数　15

（2）28の約数　1、2、4、7、14、28
42の約数　1、2、3、6、7、14、21、42
公約数　1、2、7、14
最大公約数　14

---

たてが30cm、よこが45cmの長方形の紙があります。この紙から同じ大きさの正方形を紙が余らないようにに切り取ります。正方形をできるだけ大きくするには、1辺を何cmにすればよいでしょうか。また、このとき何枚の正方形を切り取ることができますか。

■ 解法
約数・公約数・最大公約数の意味を理解するために、まずは、原始的な方法で考えてみます。
まず、1辺が1cmの正方形を切り取ることを考えてみましょう。
たて30個、よこ45個の合計30×45＝1350個の正方形を切り取ることができます。

	よこ45個
たて 30個		30cm
	45cm

次に1辺が2cmの正方形を切り取ることを考えてみましょう。
たては15等分することができますが、横は45cmなので、等分することができません。
言いかえると、45は2で割り切れないのです。

次に、1辺が3cmの正方形を切り取ることを考えてみましょう。
たて10個、よこ15個の合計10×15＝150個の正方形を切り取ることができます。
言いかえると、たて30cmもよこ45cmも3で割り切れるのです。

	よこ15個
たて 10個		30cm
	45cm

では、1辺が4cmの正方形ではどうでしょうか？
たてにもよこにも余りがないように切り取ることができません。
言いかえると、たて30cmもよこ45cmも4で割り切れないのです。

1辺が5cmの正方形ではどうでしょうか？
たて6個、よこ9個の合計6×9＝54個の正方形を切り取ることができます。
言いかえると、たて30cmもよこ45cmも5で割り切れるのです。

	よこ9個
たて 6個		30cm
	45cm

同じように、1辺が6cm、7cm、8cm・・・・14cmでは、あまりを残さずに切り取ることができません。
1辺が15cmの正方形は
たて2個、よこ3個の合計2×3＝6個の正方形を切り取ることができます。
言いかえると、たて30cmもよこ45cmも15で割り切れるのです。

	よこ3個
たて 2個		30cm
	45cm

このように考えていくと、30でも45でもわりきることができる数、つまり、30と45の公約数であれば、紙が余らないように切り取ることができるのです。一番大きな正方形は最大公約数が1辺となる正方形だから、
30と45の最大公約数（求め方は問題1参照）、つまり、1辺が15cmの正方形が正解です。

■ 答え：15cm、6個

---

りんご28個とみかん42個の両方を、できるだけ多くの子供に平等に分けます。余りがないように分けると、何人の子供に分けることができますか。

■ 解法
りんごとみかんを1人に分ける場合は、りんご28個、みかん42個となります。
2人に分ける場合は、りんご14個ずつ、みかん21個ずつとなります。
3人に分ける場合は、分けることができません。なぜでしょうか？みかんは14個（42÷3）ずつ分けることができますが、りんご28個を3人に等しく分けることができないからです。言いかえると、28は3でわり切れないからです。
4人に分ける場合も、分けることができません。りんごは7個（28÷4）ずつ分けることができますが、みかん42個を4人に等しく分けることができないからです。言いかえると、42は4でわり切れないからです。
同じように、考えていくと、5人の場合も6人の場合も分けることができません。
7人の場合は、りんご4個ずつ、みかん6個ずつで分けることができます。言いかえると、28も42も7で割り切れるからです。
ここまでくると、気がつくと思いますが、子供たちに余りのないように平等に分けるためには、28でも
42でも割り切れる数（人数）、つまり、28と42の公約数でなければならないのです

分ける人数	りんご	みかん
1人	28個	42個	…1(人)は28と42の公約数
2人	14個ずつ	21個ずつ	…2(人)は28と42の公約数
3人
4人
5人
6人
7人	4個ずつ	6個ずつ	…7(人)は28と42の公約数
8人
9人
10人
11人
12人
13人
14人	2個ずつ	3個ずつ	…14(人)は28と42の公約数
15人以上

結局、りんご28個とみかん42個の両方を、できるだけ多くの子供に平等に、余りがないように分けるためには、28と42の最大公約数（求め方は問題1参照）を求めればよいことになり、14人が正解です。

■ 答え：14人