2023.06.25

授業で数学的な考え方の育成につながる私の方法！「先に答えを確認する」

算数の授業で計算のしかたについて考える時に皆さんはどのようにしていますか？答えが分かればよいと考えている子たちにとっては、計算のしかたを考えることなかなか気が向かない場合もあります。早く答えが知りたいからです。クラスのほぼ全員が同じ答えの時は、先に答えを確認する方法があります。答えを先に確認すると、子どもは計算の仕方について考えることに集中できます。

東京学芸大学附属大泉小学校　教諭　神保　勇児

6年生の分数÷分数

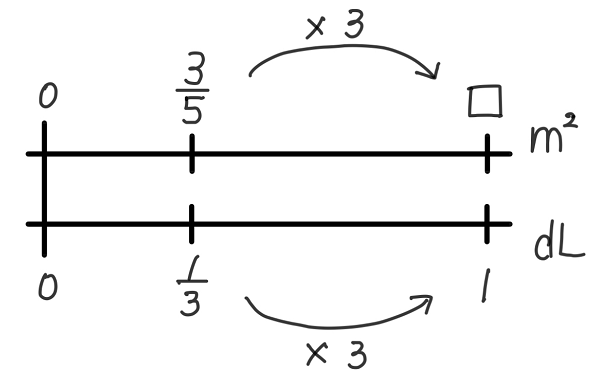
数直線図

例えば、6年生の分数÷分数の問題です。
1/3dLで3/5㎥ぬれるペンキがあります。
このペンキ1dLでぬれる面積を求める式をかきましょう。

自力解決をした後、先生が「答えは何になりましたか？」とたずねます。すると、子どもは「9/5」と答えます。そこで、「みんな同じやり方なの？」と続けてたずねてみましょう。子どもは、式や図などで解決した方法を発表します。

この問題の式は下のようになります。

3/5÷1/3＝3/5×3＝9/5

しかし、子供によっては、次のように解決する子もいます。わり算の性質を使った解決方法です。

3/5÷1/3
=(3/5×3)÷(1/3×3)
= 3/5×3÷1
= 3/5×3
＝9/5

ここでは、3/5÷1/3の割る数の1/3を1にするために3倍します。しかし、割る数だけ3倍にすると、答えが変わってしまうので、割られる数も3倍にするのです。それが、(3/5×3)÷(1/3×3)です。(1/3×3)は1になるので、3/5×3÷1となります。結果、3/5÷1/3 は3/5×3となるので、答えは9/5です。
また、数直線図を使って解決する子もいます。この図では、3/5÷1/3＝3/5×3＝9/5となります。どうしてこの式になるかというと、1/3dLを1dLにするために、ペンキの量を3倍にするからです。すると、ペンキで塗れる面積も3倍になります。ですから、3/5×3とすることができます。

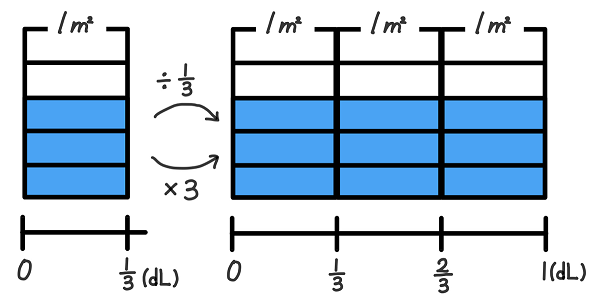
面積図

また、面積図を使って考える子もいます。1/3dLで3/5㎡塗れるペンキを3倍すると、1dLの場合の塗れる面積がわかります。ですから、式は3/5÷1/3＝3/5×3＝9/5となります。1/3dLを3倍すると、塗れる面積も3倍になることを確認します。

式で解決する方法、数直線図を使う方法、面積図を使う方法の3種類が発表されました。ここで大切なことは、それぞれの考え方の共通点を見つけていくことです。この場合は、1/3dLを3倍にすること、3/5㎡を3倍にすることが共通した考え方です。「式でも数直線でも面積図でも同じことを考えているんだね。」とまとめていくようにするとよいでしょう。

このやり方で注意しなければならないことがあります。それは、クラスの子どもの答えが何種類かある場合です。この場合、計算の仕方というよりも、どれが正しい答えなのかをみんなで考えます。そのうちに、「どうやって計算したの？」と子どもがつぶやいてくれます。このつぶやきを見逃さずにうまく取り上げて、計算の仕方を考えていくとよいでしょう。

今回のお話はいかがでしたか？この内容は、授業スキルアップ研究会でも扱っています。また、授業に関する内容は、『子どもがなぜか話したくなる　算数ファシリテーション入門』（東洋館出版社）や『学び合いコーディネートスキル60』（明治図書）もぜひ参考にしてみてください。

参考資料

神保　勇児（じんぼ　ゆうじ）

東京学芸大学附属大泉小学校　教諭

2020年度はコロナウィルスでの休校期間でオンライン授業を多く行うことがありました。その時に得た、オンラインでも使える問題の見つけ方、子供の自力解決の見取り方、つぶやきの拾い方、発表検討のさせ方など紹介していきます。
「jimbochanのブログ」https://jimbochan.hatenablog.com/