2021.03.22

算数科　つまずきを乗り越える授業づくり〜抽象化におけるつまずき〜（３）

「授業では問題を解くことができているのですが、問題が変わると解けないのです」。
教員１年目の私は、個人懇談会の際に、このように子どもの状態を伝えたことがあります。このような経験は、多くの教員が経験することだと思います。この状態は、単に学習内容を忘れているだけと言えるかもしれません。しかし、抽象化につまずきがあると捉えると授業に工夫が生まれます。今回は、抽象化を行う場面である「まとめ」にスポットライトを当てていこうと思います。

名古屋市立御器所小学校　教諭　松田翔伍

授業における「まとめ」の活動の意義

授業用語の「まとめ」。個々の先生によってその言葉が指す概念は異なると思います。多くの場合、まとめは、学習内容を振り返って、大切なことを言語化する行為です。

例えば、４年「面積」の学習では、複合図形（L字型など）の面積の求め方を考えます。複合図形を切ったり、ないものをあるとみたりする考え方が出てきます。そのどの考え方も既習の長方形の面積の求め方を使っていることに気付かせ、まとめます。「図形を切ったり加えたりすると、長方形の面積の求め方が使える」といったように、まとめることが多いと思います。私が昨年度この教材で授業を行った際には、「２つの長方形の足し算、引き算として考える」とまとめました。

まとめる意義は、知識の節約です。L字型の面積を求めて得た知識を、他の複合図形の求積でも使える知識へと高めるためにまとめを行うのです。まさに、「一を聞いて十を知る」学びです。

「まとめ」は抽象化によって行われる

抽象化とは

ここで、まとめを子どもの思考から眺めてみます。先程のL字型の求積の学習を例に、ある子の頭の中を覗いてみます。その子は、長方形なら求められることに気付き、どうにかその知識を使えないかと考えだしました。そこで、これまで図形を分けたり加えたりした経験を想起し、試しに１本線を引きました。すると、長方形２つ分になりました。しばらくして、なんとか問題を解くことができました。

次に学級の仲間の解決方法を知りました。ここまでは、それぞれの解決方法につながりは見えず、それぞれが具体的な方法として見えています。

ここで、先生が、「それぞれの考え方に共通点はあるかな」と問い掛けました。それぞれ別々に見えていた解決方法が、「長方形をつくる」という目的から見れば同じであることに、次第に気付きました。

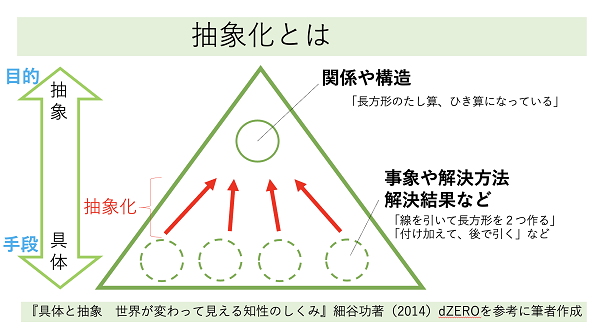
具体的な方法をまとめて１つに扱うという思考は、抽象化をしていると言ってもよいでしょう。抽象化とは、「複数のものをまとめて、一つのものとして扱う」思考を指します。（『具体と抽象　世界が変わって見える知性のしくみ』細谷功著より）「長方形を組み合わせた図形なら面積が求められる」と適用範囲を明確にし、知識を他の場面でも使える知識へと高めるためには、抽象化して言葉でまとめることが大切です。

抽象化におけるつまずき

上の例のように、きれいに抽象化が進んで、他の場面でも使える知識へと高めるのは容易ではありません。その原因は、以下のことが考えられます。

・複数の解決方法を理解していることが前提である。

・抽象化が得意な級友の発言を、ノートに写すだけになっている可能性がある。

・共通点をまとめるには、目的や視点（数学的な見方）を自覚する必要がある。
（「習った長方形の面積の求め方を使うためには」という目的が必要）

・多くの場合、抽象化は目には見えない関係や構造を扱っている。
（複合図形の求積は、長方形の足し算、引き算であることが見える化しやすい教材）

などです。
ここで挙げた以外にも、原因はあるでしょう。子どもの実態からその原因を探っている最中ですので、まとまったら報告したいと思います。

まとめの視点を明確にするための導入の工夫　似た構造の問題を同時に提示する

出会い算と追いつき算を同時に扱う

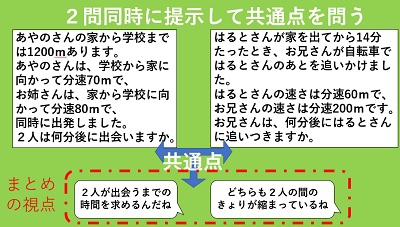
算数の５年生の教科書に、いわゆる出会い算と追いつき算が掲載されていました。似た構造の問題です。２問を同時に提示し、共通点と相違点を尋ねました。
「２人の出発点が違うね」「進む向きも違うよ」「でも、どちらも２人が出会うまでの時間を求めるんだね」このように、２問を同時に提示したのは、塾などで先行学習している子も算数が苦手な子も、同じ立場で問題把握する時間になると考えたからでした。

私は、「時間が経つに連れて変化するものは何かな？」と焦点を絞って考えさせる発問をしました。「時間が経つと、どちらも２人の距離が縮まるよ」と、何とも素敵な言葉で返ってきました。「１分でどれだけ縮まるかが違うね」「それが分かれば解けるよ」というやりとりを経て、いざ問題に取り掛かりました。ここまで20分です。

このように、２問を同時に提示したことで、「１分間で縮むきょり」に着目すれば解けそうだという見通しをもたせることができました。数学的な見方への着目です。「１分間で縮むきょり」は、まとめの際の視点になります。
問題の解決方法を共有した後に、「学習したことで、大切なことは何ですか？」と問いました。すると、この共通点に気が付く子どもが増えました。次回は、この授業でのまとめの様子を詳しく書いていこうと思います。