2021.03.02

算数科　つまずきを乗り越える授業（２）

片桐重男氏は、『算数授業研究６　つまずきを生かす指導』の中で次のように述べています。

---------------------------------------------
そもそも問題解決というのは、ある障害、つまずきに遭遇するところから始まる。これを意識しこれを何とか解決したいということから始まるのである。（片桐重男編著、1982年、明治図書）
---------------------------------------------
算数では、問題解決が多くの教室で行われています。問題はクイズとは異なります。元々頭の中にある知識を引き出すだけではなく、つまずきを乗り越えることこそが、本来の問題解決なのです。今回は、子どもたちがどの学習段階でつまずくか、そして、そのつまずきを乗り越える力をいかに身に付けさせるかを考えていきます。

名古屋市立御器所小学校　教諭　松田翔伍

つまずきの種類

前回は、つまずきの心理学的要因を『つまずきを生かす授業』（駒林邦男他著、1983年、明治図書）から考えていきました。今回は、さらに算数の学習過程のつまずきに着目していきます。

片桐氏は、先ほどの著書の中で、つまずきを次のように分類しました。

つまずきの分析－つまずきにはどんな種類があるか

（１）不注意によるつまずき
（２）理解や技能が不十分なための誤り
（３）内容を誤って理解してしまっているために正しく適用できないことによるつまずき
（４）理解していないための誤り
（５）既習内容を理解しているがこれを用いることに自信がない場合

つまずきには多様な背景があるということがわかります。そして、つまずきの種類によって、それを乗り越えさせるための手だては当然変わってきます。例えば、不注意によるつまずきは、「これは間違いだよ」と伝えるだけで、子どもがどのように修正すればよいか気付く程度のつまずきです。「うっかりミス」は、このタイプのつまずきでしょう。指導者が指摘すればよいのですが、大切なことは子ども自身が、不注意に気付くことができる力を身に付けることです。

どの段階でつまずくか

さらに片桐氏は、子どもたちが学習段階のどこでつまずくかを次のように整理しました。

（１）新しい章や節の中心となる課題を解決していく段階でのつまずき
（２）この解決をきっかけにして、新しい概念を形成したり、新しい技能を身に付けたり、その解決で有力なはたらきをした数学的な着眼の仕方、数学的方法、即ち、数学的考え方に注目するといった段階でのつまずき
（３）これらの概念や技能や考え方を新しい問題に応用して、これらを一般化し、問題解決の能力を伸ばす段階でのつまずき

よりシンプルな言葉にするならば、

①　問題を解決している段階でのつまずき
②　問題を解決した後の段階でのつまずき
③　新たな問題を発見する段階でのつまずき

になるでしょうか。

具体から抽象する際のつまずき　③　新たな問題を発見する段階でのつまずき

算数の学習は、問題を解いて終わりではありません。複数の考え方の共通点を見付けてより本質的な考え方を明確にしたり、問題の考察の範囲を広げて発展的に考えたりして、新たな問題を発見することが、指導要領の中でも期待されています。

５年生で、三角形の内角の和を求めたり、多角形の内角の和を求めたりする学習があります。様々な三角形の内角の和を調べ、どれも180°になることから、「三角形の角の大きさの和は180°になる」とまとめるのが多くの教室で行われている授業です。しかし、この段階で、「三角形の角の大きさの和は、どれも180°になる」というように、知識を一般化することにつまずいている子も見受けられます。これが具体から抽象する際のつまずきです。調べている三角形は具体です。いくつかの具体から、「どの三角形の内角の和も180°になる」と共通点を抽象することにつまずくのです。

では、どうすればこのつまずきを乗り越えさせる力を身に付けさせることができるでしょうか。

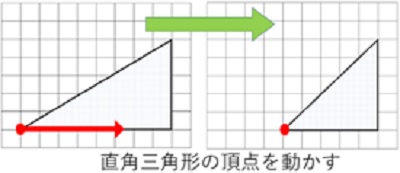
私は、まず、特殊な場合である直角三角形を、右のように１つの頂点だけを動かして提示しました。図を見て変わったことに着目し、角の大きさの変化に着目し始めた子どもたち。ここから、実際に提示した直角三角形を配布し、角の大きさの和を調べていきました。

まずは、分度器を使って調べた角の大きさを表にまとめていきました。すると、測定の誤差により179°や181°という結果が出てきました。

次に、直角三角形を敷き詰めて、橋を作り、真っすぐな橋になることから、絶対に180°になるという意見が出てきました。前時に三角形を使った敷き詰めを学習していたので、その知識を使ったのですね。「絶対」という言葉が、すてきだと思いました。

続いて、合同な直角三角形を２枚組み合わせて、長方形を作る考えを子どもは発表しました。長方形の角の和は360°。その半分が180°だから、絶対180°になると言いました。ここで、学習を振り返ってまとめました。

「直角三角形の３つの角の和は180°になる。」

このように板書すると、子どもたちは少々むきになって発言してきました。

「直角三角形じゃなくても180°になると思います」

中には、塾などで先取りした子もいます。私は、「他にも180°になる三角形は確かにありそうだね」と少しずれたことを言ってみました。子どもたちは、「全部の三角形です！！」とさらにむきになりました。しかし、実際に実験したわけではないので、「細長い三角形は、どうなるのだろう？」と素直に問う子も現れました。そして、実際に細長い三角形の内角の和を調べました。

この授業のように、算数で学習する知識は、その適用範囲をはっきりと意識することが、具体から抽象へのつまずきを乗り越えるために大切なことです。