2020.08.07

救世主が現れた！４年「変わり方」

今回は、算数の学習で「見えない同じ」を発見させていく授業をした際の出来事を紹介します。発見する喜びを多くの子が味わう授業には、救世主が現れることがあります。私が言う救世主とは、いきいきと自分の考えを語り、周りの子の発見を促す人物のことです。本実践は、筑波大学附属小学校の盛山隆雄先生の実践の追試です。（「算数授業研究」2019年vol.122、東洋館出版社に掲載）

名古屋市立御器所小学校　教諭　松田翔伍

あみだくじ　最低で何本の横線をくわえるとよい？

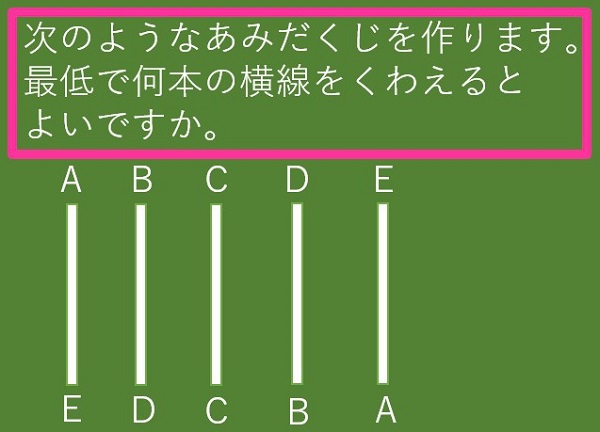
最低の本数であみだくじを作るには？

右の図は、人数を増やしていくと、あみだくじの横線の数の増え方にきまりが見付かる面白い問題です。さて、４年生の子どもたちに、５人用のあみだくじを提示しました。「難しそう」と思わせた後で、少ない人数から調べていくことを提案しました。

あみだくじが２人用の時から調べさせました（ここがこの授業がドラマチックになったターニングポイントだったと思います）。そして、３人用、４人用の時……と調べていきました。その結果を付箋にメモさせ、それを整理することで、「横線の増え方」という数学的な見方に気付かせていきました。この見方に気が付けば、「人数が増えていくにつれて、あみだくじの横線の増え方も＋１になる」という「見えない同じ」を自ら発見させることができると考えたのです。

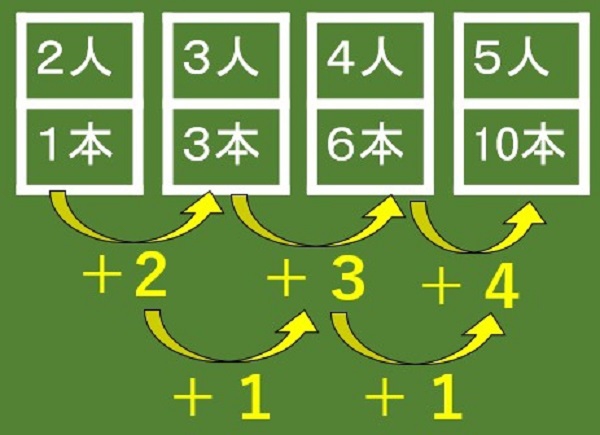
「見えない同じ」に気が付きましたか？

４人用のあみだくじを調べ終わった場面です。ある子を指名すると、その子は黒板に矢印を書き込みました。「ああ！」という声が広がりました。次に、ある子が「＋２、＋３と増えている」と言います。すると、別の子の「その下にもある！」と言う声が聞こえてきました。

「＋２、＋３」の下にも矢印と「＋１、＋１」と書いてくれました。多くの子が「見えない同じ」を発見することができたようでした。私は、「何か気が付いたみたいだね」と全体に声を掛けました。多くの子が、「見えない同じ」を発見したようでした。

しかしです。私の声掛けを受けて、一人だけ、表情を曇らせた子がいました。その子は、黒板を見ながら「う～ん……」と、うなっています。まだ、「見えない同じ」を発見できていなかったようでした。

救世主、現る！

授業の様子

私は、「まだ発見していない子もいるみたいだから、ヒントを出せる人はいますか」と投げ掛けました。しかし、黒板には、十分ヒントになることが書いてあります。そこから、どのような説明があればよいのか正直私には分かりませんでした。

そんな私の不安など、全く気にせず救世主が現れました。「もしもね、１人用のあみだくじを考えたとするでしょ？１人用の時は、横線が０本でしょ。だから、ここが＋１なの」と説明しました（板書写真の赤線囲みの部分）。あの子の曇った表情もどんどん晴れていることが分かりました。

この後、５人の場合が10本でできることを確かめた後で、「じゃあ次は……」と言うと、あちこちから「６本の時を調べたい」、「10本の時を調べたい」という声があがりました。

救世主は、なぜ現れたか

私は今回、簡単な場合から調べさせました。それは、あみだくじが成立する最低人数ということで２人用から。今振り返れば、１人用から考え出すのが自然です。しかし、余白があったからこそ、救世主が現れたのだと思います。意図的に仕掛けていれば……。授業の難しさと面白さを体感した授業になりました。

もう一人いた救世主

教材についてもう少し書こうと思います。私がこの教材を使って「変わり方」の授業をしようと思った一番のポイントは、試行錯誤しなければ横線が何本必要か分からないからです。一般的に扱うマッチ棒で四角形を作るような教材は、本数を数えれば答えが分かってしまう。それは、よさでもあるのですが、答えが見えていないからこそ、きまりを使って問題を解こうという思いが生まれると思うのです。

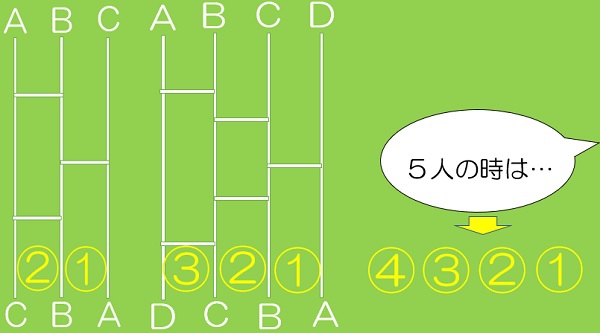
あみだくじの法則

きまりから考えれば５人用のあみだくじの横線が10本になります。しかし、１０本になることを確かめるまで納得には至りませんでした。

ここで救世主が現れたのです。横線の数が最小になる場合の横線の書き方を、きまりを見出して発見して発表してくれた子がいたのです。その子は、図ように、黄色い丸囲みで数字を板書していきました。そして、「５人の時は、４，３，２，１本の横線を書けばいいんじゃないかな？」と発表してくれました。

子どもの発想って、本当に面白いです。私の発想を簡単に超えてきます。こんな姿に出会えるのも、発見の喜びのある「見えない同じ」を扱った授業の醍醐味です。