2020.07.17

「見えない同じ」が見えてくる仕掛け

「あ！」「おお！気付いちゃったよ！」。
子どもたちが、「同じ」を自ら発見した時の表情を見ると、自分までうれしくなってしまいます。
今回は算数の学習で、「同じ」を自ら発見させるための仕掛けをご紹介します。

名古屋市立御器所小学校　教諭　松田翔伍

仕掛け①　トピック教材で「同じ」ことの面白さを体験させておく

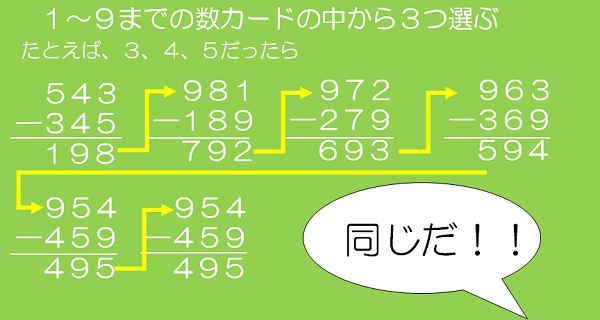
１～９までの数カードの中から好きな数字を３つ選んでください。その３つのカードを大きい順に並べて作った３桁の数から、小さい順に並べて作った３桁の数を引きます。その差の数字を先ほどと同じように、大きい順に並べて作った３桁の数から、小さい順に並べて作った３桁の数を引きます。それを繰り返していきます。

何か気付くことは、ありませんか？何回か続けていくと、「４，９，５」という数字が必ず出てきます。これは、とても有名な教材で、「４，９，５」は『カプレカ数』と呼ばれています。この教材を使って授業をすると、子どもから自然と、「同じだ！」、「面白い！」という声が生まれます。経験上、子どもたちはまず差の十の位が「９」になるという「同じ」に気付くでしょう。これは、「見える同じ」です。まずは、「見える同じ」の発見を思いっきり褒めて価値付けます。次に、「何回計算したら４，９，５が出てくるかな？」や「選ぶカードを４つにしたら、どうなるかな？」という問いも出てきます。

こうしたトピック的な教材は、余分な時間が掛かってしまい、扱いにくいという方も多くいます。しかし、共通点を見つけようとする見方や問題文の数値を広げて発展させていこうという考え方を育む時間は、大きな価値があると思います。

仕掛け②　整理してもいいですか？という声を生むために、ばらばらに提示する

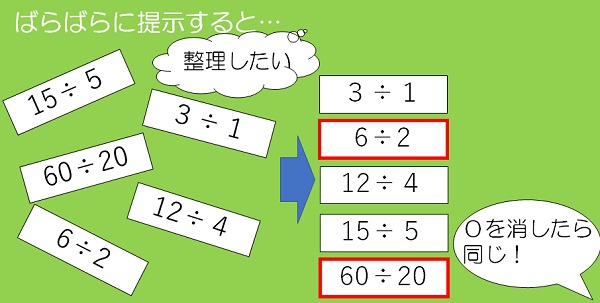
４年生の子どもたちとの授業。割られる数と割る数に同じ数ずつ掛けたり割ったりしても、商は変わらないことを発見させる授業です。まず、「商が３になる式を書きましょう」と投げ掛けて、短冊に式を書かせました。そして、30人弱いる教室の子どもたち全員に１つずつ式を書かせます。そして、その短冊をばらばらに黒板に貼らせます。

ばらばらに提示すると、子どもたちから「整理してもいいですか？」という声が出てきました。その声に乗っかって、整理させてみます。「きまりを見つけた！」と声が出てきたら最高です。見つけたきまりについて発表させてみると、この時は６÷２と60÷20の式を見て、「０を消したら同じ式になります」と言いました。別の子がその発言に続けて、「割られる数と割る数の両方とも10倍しています」と言いました。

割り算の性質は、「見えない同じ」そのものです。ばらばらにカードを並べることで、子どもたちの「整理したい」という思いをくすぐり、実際に整理させることで、式と式の関係に着目させることができました。この提示の仕方は、和や差が一定の場合の式を扱えば１年生の「たしざん」「ひきざん」の学習にもなります。

仕掛け③　実は「同じ」状況を作る

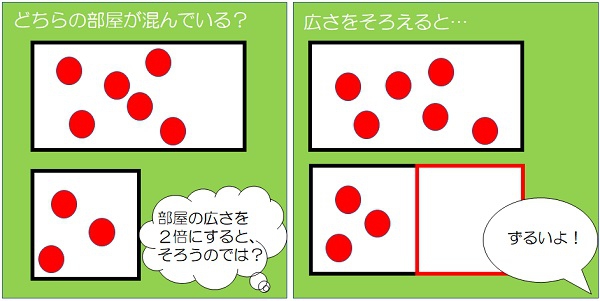
この仕掛けは、４年「小数倍」や５年「単位量あたりの大きさ」「割合」など、目には見えない概念を扱う授業と相性の良い仕掛けです。例えば、５年「単位量当たりの大きさ」の学習で、このような２つの部屋の混み具合を比べる場面を与えます。子どもたちは、混み具合を比べる際には、広さと人数の２つの量で比べるとよいことに気付き、そのどちらかが揃っていれば比べられることを理解した状況です。２つとも揃っていない状況ですので、「どちらかを揃えよう」という見通しを持たせます。

今回は、このように上下に部屋を見せたことで、感覚で下の部屋の広さの２倍が上の部屋の大きさだと分かった子どもたち。ある子が、「下の部屋をもう一つ加えれば、上の部屋の広さに揃って比べられると思う」と発言しました。「いいねえ！じゃあ……」と言って部屋を加えます。そして、「下の部屋の方が空いているね」と言ってみました。すると、「いや！だめだよ！ずるい！」の声が。「どういうこと？」と尋ねると、「下の部屋の広さを２倍したでしょ。そうしたら、人数も２倍にしなくちゃいけない」と比例関係を仮定する考え方が現れてきました。ここで、実際に人数を２倍すると、広さも人数も揃うという数値設定にしておくことがポイントです。一見すると異なる事象が、比例を使うと「同じ」に見えてくるという状況を作ることで、子どもたちは、「混み具合が同じ」という「見えない同じ」に気付き始めました。「なんだ～！同じ混み具合じゃないですか～」。子どもたちから、安心したような言葉があふれてきたことが印象的でした。

広さと人数を同じ数だけ掛けたり割ったりしたときに、両者が揃うときは同じ混み具合にしようという理解が進んだのでしょうか。この後、授業は、公倍数の考え方や１当たりの大きさに揃える考え方が出てきました。