2020.06.30

「全部、平行四辺形になる」図形の見方をアップデート

長方形の面積公式を基にして、直角三角形、鋭角三角形、四角形、鈍角三角形、平行四辺形、台形の順（教科書会社によって違いあり）で面積の求め方を学習していきます。学習が進むにつれて、「三角形＝底辺×高さ÷２」、「平行四辺形＝底辺×高さ」、「台形＝（上底＋下底）×高さ÷２」の３つの公式を新しい知識として学ぶことになります。

しかし、いざ問題を解く段階になると、「÷２をするのかな、いらないんだっけ」と迷ってしまい、実際に間違えてしまう姿も多く見られます。これまでの学習で働かせた図形の見方とこれらの公式の知識が引き離されてしまっていることが原因です。そこで、台形の面積の求め方を学習する際、これらの知識を統合するために振り返る活動を取り入れた実践を紹介します。

名古屋市立御器所小学校　教諭　松田翔伍

どの図形の面積が一番大きいですか？

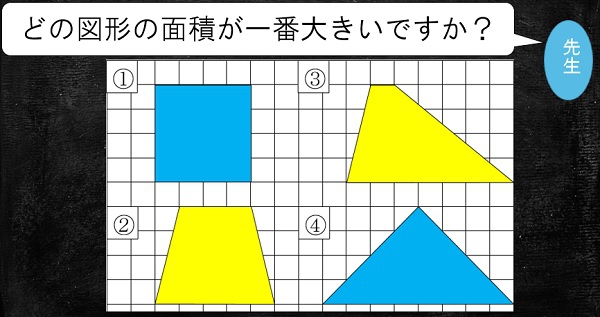
次の図形を一度に見せて、「どの図形の面積が一番大きいですか？」と問い掛けました。「①の正方形と④の三角形は計算で求められます」とつぶやく子どもたち。実際に計算して調べてみると、両方とも１６㎠になります。②と③の図形は面積の求め方を学習していない台形です。

「①と②は形が似ている」という反応があったので、「比べてみようか」と投げ掛けました。「どのように比べるか」と問い掛けると、「重ねてみる」と言います。重ねて、はみ出た部分を切り取って……素朴な考え方ですが、等積変形の考え方の復習にもなり、②の図形が①の正方形と同じ形に等積変形できることを共有しました。問題は、③の台形です。④の図形と重ねてはみ出た部分でも比べにくい。この台形の面積の求め方を調べることが本時の課題であること焦点化しました。

一人で考える時間を取ると、様々な解決方法が出てきました。この多様性が台形の面積の学習で面白いところ！！しかし、この日の授業で私は２種類の方法しか取り上げませんでした。ここは私の反省。子どもたちは、たくさんの方法で解くことを面白がりました。次の日に、「昨日はたくさんの方法で解いていました。一体いくつの方法があるかな？」と言って、たくさんの方法を出すことを課題としました。

振り返り活動　高さが全部同じ！上底と下底の和も同じ！

さて、話を戻します。２種類の基本的な考え方を共有しました。結果は、16㎠。すべて同じ大きさです。ここで、「すべて16㎠だなんて、偶然だね」と偶然性を問い掛けました。偶然もなにも、私が問題設定しているのですから、ある子は「先生は16㎠が好きなんだね」と言いました。偶然性を問う状況をいかに作るかも私の授業の課題です。

別の子は、「高さが全部同じなんだよ。だから、全部同じだ」と図形の構成要素に着目しました。ここで、「共通点を見付けたんだね！高さが同じなら面積はすべて同じになるんだね」と、とぼけてみました。すると、「そういうわけではないけれど……」「②の台形も同じなんだけど、上底と下底を足したら８になります」と、上底と下底の和に着目する子が出てきました。

三角形も同じだ！！！

「あ！！」と驚くような声があがりました。その子は、「三角形も同じだ！！！」と興奮気味に語ろうとしました。「三角形も上底を０㎝と見れば同じだよ」とその子が言うと、「なるほど」と納得が広がっていきました。

そして、三角形を２枚使って、平行四辺形に倍積変形することができることも説明してもらいました。ここでチャイムが鳴りました。学習感想には、「全部、平行四辺形になることが分かった。面白い」と書く子どももいました。

課題は山積みだが

今回紹介した実践では、これまでに学習したすべての図形が、倍積変形すると平行四辺形になることを子どもたちが発見していきました。「２枚組み合わせる」という図形の見方と、「それらを半分にするから÷２をする」という考え方を結び付けることで、確かな知識へとアップデートすることができると思います。しかし、これまでに述べたように課題も山積みです。次の時間には、本当に多様な解決方法が出てきました。台形の求積という教材の価値も多様であるとともに、子どもにとって面白いと感じることこそ大切にしていきたいと思います。