2020.04.13

「見えない同じ」を発見する！考える楽しさを味わう算数学習

算数の難しさは、目に見えにくいことを扱うことにあります。しかし、目に見えにくいものの中にある「同じ」は、算数の面白さそのものでもあります。この「見えない同じ」を自分で発見したという経験が、考える楽しさを味わうポイントだということを、実際の授業での子どもの姿で書き綴っていきます。

名古屋市立御器所小学校　教諭　松田翔伍

「できる」けど、「楽しくない」算数授業からの脱却

はじめまして！松田翔伍です。
考える楽しさを味わう算数学習を目指して、教師修行真っ最中の教諭です。

算数は「分かる」「できる」がはっきりする教科です。
ですので、まずは子どもたちに「できるようにさせることが大切だ」。
このような考え方で算数を教えている大人が、多くいるように感じます。
私はその思いを否定しません。
確かに、「できた」喜びが、算数好きになるきっかけになることもあります。
しかし、その考え方は間違いだと考えます。
私自身もそのようにして、子どもたちに何度も嫌な思いをさせてしまった苦い経験があるからです。
「できる」は、「楽しい」という感情に必ずしも結び付きません。
私の経験則から述べると、教師から子どもへの知識伝達型の授業になると、その傾向は顕著になるようです。
「できる」けど、「楽しくない」。
教諭一年目の私はそんな言葉を何度も聞いて、ひたすら「どうすれば算数の学習を楽しいと思ってくれるか」と、考え続けました。

もう少し、「楽しくない」の中味について触れます。

高学年になると、算数嫌いの児童が増えると耳にしたことがあります。
そうなってしまうのは、高学年の学習内容が、割合や速さ、比など、目には見えにくい数と数の関係についての学習になって、扱う内容が抽象的になってくることが原因だと考えます。
目には見えないことを扱うので、数に表した時の実感がわかない子もいます。

しかし、「目には見えにくいこと。これは、算数の面白さでもあるのではないか？」と、子どもたちと授業をしていく中で考えるようになりました。

「見えない同じ」を発見した花子さん

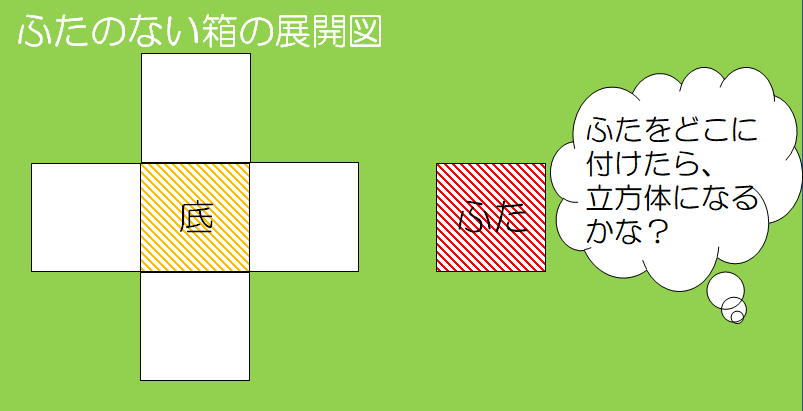
数年前に４年生の子どもたちと立方体の展開図は何種類あるのか考えていった時のことです。
前時に、ふたのない箱（それぞれの面は正方形）の展開図を考えました。
ふたのない箱は、面の数が５つです。
立方体よりも展開図を考えるハードルが下がります。
このアイデアは、筑波大学附属小学校の夏坂哲志先生の実践を参考にしました。展開の仕方は自分なりにアレンジして授業に臨みました。（夏坂哲志『夏坂哲志の算数授業のつくり方（プレミアム講座ライブ）』東洋館出版社、2012）

「立方体の展開図は、ふたのない展開図と比べて種類は多いでしょうか？少ないでしょうか？」
このように投げ掛けると、子どもたちは、
「面の数が増えるから、立方体の展開図の方が多いと思います」
と言います。

工作用紙を使って調べてみることになりました。
様子を見ていると、花子さん（仮名：以下子どもの名前はすべて仮名）が難しそうな顔をして、じっとしています。
「面が増えたから難しい」
このつぶやきを聞いた、太郎くんが、
「大丈夫！昨日のふたのない展開図をもとにして考えていけばいいんだよ」
と言い出しました。
「なるほど！いいね！いいね！」
周りの子たちもこの意見に賛同しました。
花子さんも、見通しが立ったようで手が動き出しました。
前日の学習を生かしている姿を褒めました。
そして、ふたのない箱の展開図を一つずつ取り出して、一緒に調べていくことにしました。
ふたのない箱の展開図のどこにふたを付けたらよいか考えていったのです。
出来上がる立方体の展開図が、すでに発見されたものかどうか調べるために、回転したり反転したりしていきます。
そして、板書に、ふたが付く辺に★マークを記していきました。

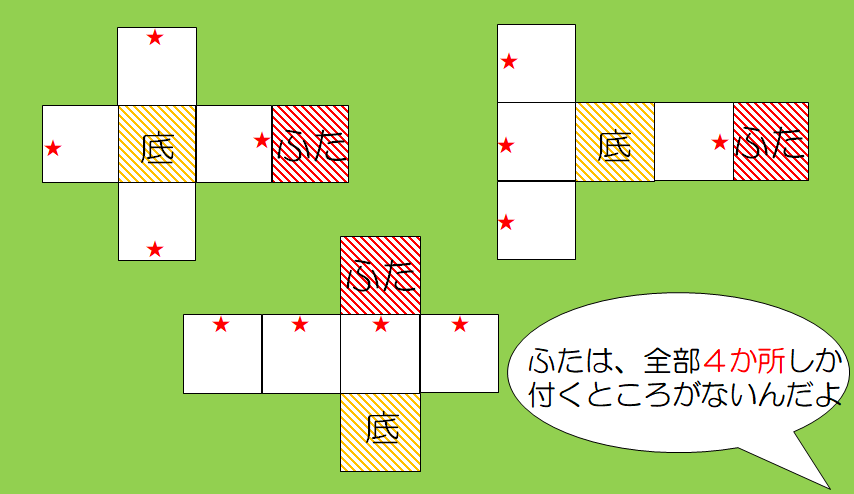
すべての展開図を発見する前に、チャイムが鳴ってしまいました。授業の後に、あの花子さんが私のところに寄って来て、こう言いました。
「先生、大発見したよ。ふたは、全部４カ所しか付くところがないんだよ」
困っていたあの花子さんが喜びの表情を浮かべていました。
そのことが、うれしくてたまりませんでした。
この花子さんの言葉を聞いた友達の由美子さんが、「なんで４カ所か分かる！だってね……」
と、説明し出しました。
ふたのない展開図を組み立ててみるとその理由が分かります。
次の時間、花子さんのこの発見をみんなに紹介しました。
花子さんの目は、誇らしげに輝いていました。

授業後に、自分の授業を振り返りました。先行実践を読み返すと、ふたが４カ所に付くことに着目させる展開になっていました。
私は、立方体の展開図の11種類すべてを子どもたちに発見させたいという思いが強かったため、授業の中でそこに着目させませんでした。
「ああ……。４カ所にしかふたが付かないことに着目させれば、子どもたちの試行錯誤する時間がもっと有意義になったのに……」と、深く反省。
先行実践を読んでも生かしきれない自分の勉強不足さを痛感しました。
また、「ふたが付く位置に★マークを付けていたことで、花子さんは全部４カ所という同じを発見することができたんだ」と、気付きも得られました。

全部４カ所というのは、むやみやたらに試行錯誤していたら、見えないままでした。私は、無意識でしたが、見えない同じを、★マークで見えるようにしていたのです。
その結果、花子さんは、その「同じ」を発見することができたようです。

算数科で大切にされてきた「同じ」

この授業で見せた花子さんの姿のように、一見異なる事柄の中にある「見えない同じ」を、子どもたちが自ら発見することができた時、宝物でも見つけたかのような表情が広がっていきます。

算数科では、もともと「同じ」ことに大きな価値を見出してきました。例えば、日本数学教育学会名誉会長の杉山吉茂先生は、次のように述べられています。
--------------------------------------------------------------------------------
「すべてのものは違っているんだけれども、違っているものの中に似ているところがあるという認識があって初めて概念ができてくるのです。似ているということは、ある観点から見ると同じと見ることができるということです。」（杉山吉茂「初等科数学科教育学序説」東洋館出版社、2008）
--------------------------------------------------------------------------------
概念とは、そもそも「同じ」を見出すことで形成されてくるのです。
また、「同じ」を見出すことで、きまりや性質も発見することができます。

そして、私は、「見えない同じ」をキーワードに授業づくりをしていけば、考える楽しさを味わわせることができるのではないかと考えるようになりました。

「見えない同じ」を自分の力で発見できた経験が、今後の学習の期待感につながる

「見えない同じ」を自分の力で発見することができたという経験があれば、高学年でぶつかる壁も「何か面白いことが見付かるかも」と期待感をもって立ち向かっていけると信じています。

教育つれづれ日誌の執筆を通して、算数を教えるすべての人が、目の前の子どもたちに考える楽しさを味わわせてみようと思えるきっかけにしたいと思います。
これからも、よろしくお願いします。