円のまわりをまわる円
ピンクの円のまわりを青い円が1周すると,青い円自身も1回転するように思われます。しかし、これは錯覚。回転する円の中心が動いたきょりで考えなくてはなりません。
問題

半径が10cmの円に顔がかかれている二つの円があります。青い円がピンクの円のまわりをすべらないようにまわります。
青い円がピンクの円のまわりを1周する間に青い円自身は何回転しますか?
解法
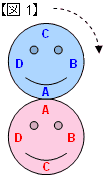
ピンクの円のまわりを青い円が1周すると,青い円自身も1回転するように思われますが,実はそうではありません。
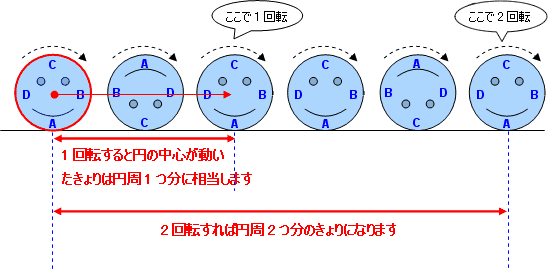
そこで青の円がすべらずに回転する様子を調べるために,【図1】のようにピンクの円を4等分する点に頭から時計まわりにA,B,C,Dとつけて,青い円にはあごの部分から,反時計まわりにA,B,C,Dと記号をつけてみます。(記号のつけかたはこの通りでなくてもかまいません)
では,調べてみましょう。
最初はピンクの頭Aと青のあごAがくっついています。
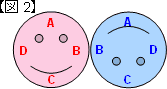
青い円をすべらずに回転させながら少し動かしてみると,【図2】のように青は回転しながら,さかさまになり,ピンクのほっぺたBと青のほっぺたBがくっつきました。
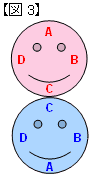
さらに,青がすべらずに回転すると,ピンクのあごCと青の頭Cがくっつきました【図3】。
ここまでで,青は一度【図2】のようにさかさまになって,また戻りましたので,青は1回転したことになります。
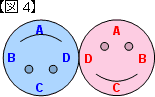
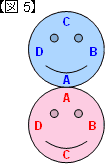
さらに回転すると,青は【図4】のようにもういちどさかさまになって,【図5】のようにもとにもどります。【図1】から【図5】を見なおしてみると,青はピンクを半周する間に1回転しています。 そして,1周すると2回転します。
ピンクの円のまわりを青い円が1周すると,青い円自身も1回転するように思われますが,実はこれは錯覚(さっかく)です。
では,どのように考えればよいのでしょうか。
結論から言うと,回転する円がどれだけ回転するかは,回転する円の中心が動いたきょりで考えなくてはならないのです。
例えば,円が平らな地面を1回転する場合,円の中心が動くきょりは円周の長さと同じになります。1回転すれば,円周1つ分の長さ,2回転すれば円周2つ分の長さを動いたことになります。
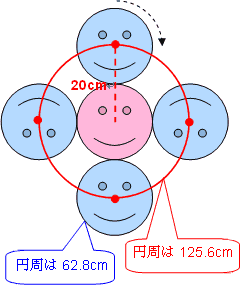
それでは円が円のまわりをまわる場合はどうでしょうか?
右の図のように,青い顔の円の中心が動くきょりは赤で書いた大きな円の円周の長さになります。
青い顔の円の半径は10cmだったので,赤で書いた大きな円の半径は20cmです。
つまり,青い顔の円の中心が動くきょりは
直径×3.14=(20+20)×3.14
=40×3.14
=125.6 cm
一方,青い顔の円の円周の長さは
直径×3.14=(10+10)×3.14
=20×3.14
=62.8 cm
よって,青い顔の円の中心が動いたきょりは,125.6÷62.8=2で,自分自身の円周2つ分を動いたことになります。
よって,青い円は2回転します。
・赤い円は青い円の中心が動くみちすじ
・赤い円の円周は青い円の円周2つ分<
◆ポイント
円のまわりを円がすべらずに回転するときは,回転する円の中心が動くきょりと回転する円自身の円周の長さを比べて考える。
答え:2回転
チャレンジ問題
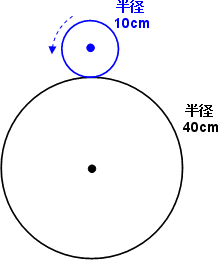
半径10cmの青い円が半径40cmの円のまわりをすべらずに1周すると半径10cmの青い円は何回転しますか?
解法
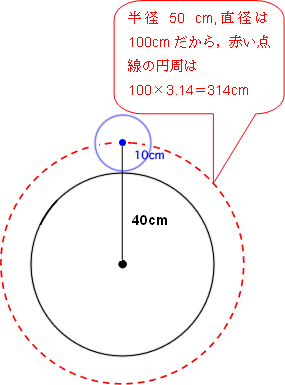
半径10cmの青い円の中心は,右の図のように,半径50cmの円周上を動きます。
動いたきょりは,
直径×3.14=100×3.14=314cm
一方,青い円は半径10cmなので円周の長さは
直径×3.14=20×3.14=62.8cm
よって,314÷62.8=5
つまり,赤い点線の円周(青い円の中心が動くきょり)は,半径10cmの青い円の円周の5つ分に相当するので, 5回転が正解。
答え:5回転

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
