道順の問題
今回は、道順の問題を説明します。道順の問題は「場合の数」に分類され、場合の数の考え方の基本となります。特にごばんの目の道順の問題は入学試験だけでなく、さまざまな検定試験などでも出題されています。
問題1
図のようにAからBを通って、Cに行く道があります。A→B→Cの道すじは何通りありますか。

解説
問題の意味さえわかれば、直接数えても、正解できそうな問題ですね。とりあえず数えてみましょう。
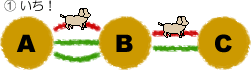





全部で6通りです。もれなく数えるということは大切なことですが、ここで学んでもらいたいことは、要領よく数える(計算する)方法です。
結論からいうと、この問題は3×2で計算できるのです。
これを説明するために道に名前をつけます。

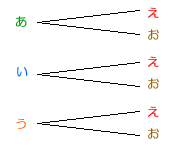
まず、あを通る方法を考えます。すると あ→え と あ→お の2通りの方法が考えられます。
次に、いを通る方法を考えます。すると い→え と い→お のこれも2通りの方法が考えられます。
最後に、うを通る方法を考えます。すると う→え と う→お でこれも2通りです。
つまり、AからBに行く方法はあ、い、うの3通りの方法がありますが、そのあ、い、う のそれぞれについて、えでいく方法とおで行く方法の2通りがあります。
3つの2通りがあるので3×2で合計6通りとなるわけです。

樹形図からも6通りになることがわかります。
AからBへ行く方法が■通り、BからCへ行く方法が▲通りあるとき、AからCへ行く方法は■×▲通りです。
答え:ア、ウ、エ、カ、キ
問題2
次の図でAからBまで遠回りしないで行く方法は何通りありますか?

解説
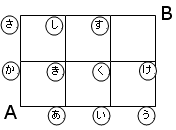
これはよく見られるごばんの目の道順です。解き方は決まっています。それぞれの交差点に行くために何通りあるかを求め、その数を書いていきます。説明のため、それぞれの交差点に名前をつけておきます。
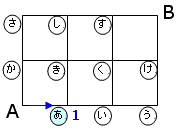
まず、Aの1つ右の交差点 の交差点に行く進み方を考えます。
の交差点に行く進み方を考えます。
遠回りしないで行くので、1通りです。
そこで のところに1と記入します。
のところに1と記入します。

A→ →
→ →
→ は遠回りなのでルール違反です。
は遠回りなのでルール違反です。
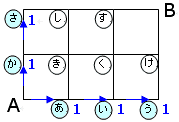
そこで のところに1と記入します。
のところに1と記入します。
同じように、交差点 への進み方も交差点
への進み方も交差点 への進み方も1通りしかありませんので、それぞれ1と記入します。
への進み方も1通りしかありませんので、それぞれ1と記入します。  も
も も同じように1通りです。
も同じように1通りです。
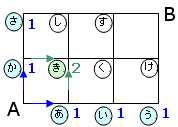
それでは、交差点 への進み方は何通りでしょうか?
への進み方は何通りでしょうか?
今度は を通ってくる場合と
を通ってくる場合と を通ってくる場合の2通りがあるので2と記入します。
を通ってくる場合の2通りがあるので2と記入します。

つまり への進み方は
への進み方は
A→ →
→
A→ →
→
の2通りです。
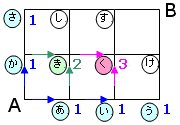
次に への進み方を考えてみます。
への進み方を考えてみます。
 を通ってくる場合が1通り
を通ってくる場合が1通り
 を通ってくる場合が2通り
を通ってくる場合が2通り
なので合計3通りあります。そこで に3を記入します。
に3を記入します。

つまり への進み方は
への進み方は
A→ →
→ →
→
A→ →
→ →
→
A→ →
→ →
→
の3通りです。
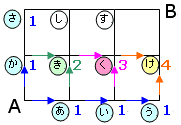
それぞれの交差点への進み方は、その交差点へ行く一つ前の交差点に書かれている数を足すと求めることができるのです。
例えば、 は
は の1と
の1と の3を足して4となります。
の3を足して4となります。
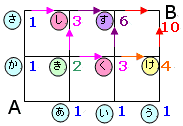
同じように考えると、 は3、
は3、 は6となります。
は6となります。
そして、最後のBは と
と を足すので、10です。
を足すので、10です。
つまり、AからBまで遠回りしないで行く方法は10通りです。
このように、ごばんの目の道順の問題は各交差点までの進み方の数を単純作業的に記入していくと解くことができるのです。
道順の問題を解くときのポイント
道順の問題を解くときのポイントはこの2つでOKです。
あとは応用問題の考え方を身につけていくことになります。
ポイント1: AからBへ行く方法が■通り、BからCへ行く方法が▲通りあるとき、AからCへ行く方法は■×▲通り
ポイント2: ごばんの目の道順の問題は各交差点までの進み方の数を記入して解く
答え:10通り
問題3
次の図のような道を最短距離で行くとき、次の問いに答えなさい。
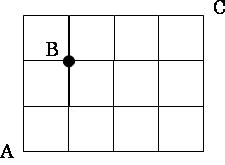
(1)AからCまで行くとき、道順は全部で何通りありますか。
(2)AからBを通ってCまで行くとき、道順は全部で何通りありますか。
(3)Bを通らないで、AからCへ行く道順は全部で何通りありますか。
解説
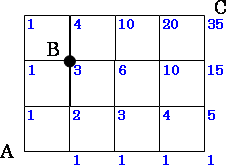
(1)ごばんの目の道順の問題です。問題2と同様にして、各交差点までの進み方の数を記入して解きます。すべての交差点に数を記入すると、次の図のようになり、AからBまで行くとき、道順は全部で35通りあることがわかります。

必ず自分で書いて試してください。
(2)AからBを通ってCまで行くときの道順は2つにわけて考えます。まず、AからBへ行く道順を求め、次にBからCへ行く道順を求めます。すると、見た目は違いますが問題1と同じになります。

先に説明したポイント1
AからBへ行く方法が■通り、BからCへ行く方法が▲通りあるとき、AからCへ行く方法は■×▲通り
それでは、まずAからBへ行く道順を求めてみます。ごばんの目の道順なので、同じように各交差点までの進み方の数を記入して解きます。すると、次のようになり3通りであることがわかります。
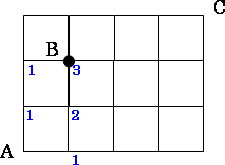
同じようにして、BからCへ行く道順を求めます。すると次のようになり4通りであることがわかります。
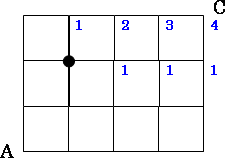
まとめると、AからBへ行く道順は3通り、BからCへ行く道順は4通りになります。
だから、AからBを通ってCまで行くときの道順は3×4=12通りです。

結局、この(2)は、次の図のような問題と同じことになります。

AからBを通ってCまで行くときの道順は3×4=12通り
(3)AからCまで行く道順は(1)で35通りとわかりました。
Bを通ってCまで行く道順は(2)で12通りとわかりました。
ゆえに、Bを通らないで、AからCへ行く道順は35-12=23通りです。
また、次のように、各交差点までの進み方の数を記入して解くこともできます。Bを通らないので、Bのとなりの交差点からBへ続く道はないものとして考えます。
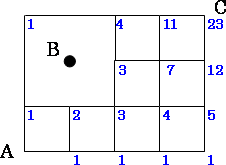
答え:(1)35通り(2)12通り(3)23通り
特別問題
(ごばんの目の道順の問題と同じ解き方でこんな問題も解くことができます)
青色のおはじきと黄色のおはじきと赤色のおはじきがたくさんあります。この中から5個のおはじきを選ぶ方法は何通りありますか。
解説
この問題をごばんの目の道順の問題を活用して解くと次のようになります。
まず、次のように図を書きます。
そして左下から右上に遠回りをしないで行く方法を考えます。
たとえば、次のように進んだ場合、青色のおはじきだけを5個を選んだ場合になります。
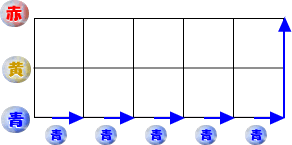
次のような場合は、青色2個、黄色2個、赤色1個の合計5個を選ぶ方法(道順)となります。
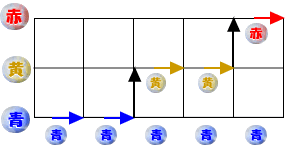
つまり、青、黄、赤をそれぞれの横線上に見て、横に進んだときにその色が数えられるという考え方です。それでは、ごばんの目の道順の解き方で交差点への進み方の数を記入していきます。
すると、次の通りとなり、21通りであることがわかります。
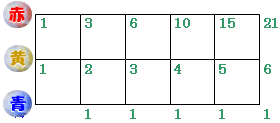
答え:21通り

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
