学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
平均算（応用編）
前回の「平均算（基礎編）」に続いて「平均算」の応用編。平均算の問題を解くときには、全部足して個数で割る、という計算的な考え方だけでなく、図形的な考え方（面積図の考え方）を知っていると、難しい問題も効率的に解けて便利です。
準備体操
今回は前回の内容を基本として応用問題を解きます。
その前に簡単に前回の復習をしておきます。 太郎君の4科目のテストの結果は、国語60点、算数90点、理科70点、社会100点でした。太郎君の4科目の平均点は何点ですか。
解法
4科目の合計は60＋90＋70＋100＝320点
平均は個数（科目数）で割って、320÷4＝80点
答え：80点
①まずは、4科目の得点をそれぞれ、次のように図（四角形）で表します。
この問題のように簡単な問題では、「たしてわるのが平均」という考え方で計算するのがベストです。しかし応用問題になると、このように簡単な計算では求めることが困難になります。そこで、図形的な考え方（面積図）が登場します。
次に、一番得点の低い国語の６０点を基準として、各科目の出ている部分に注目します。このでっぱっている部分を４科目にふりわけて、平らになるようにならして、そろえます。そして、ならしてそろえたときの高さが「平均」です。
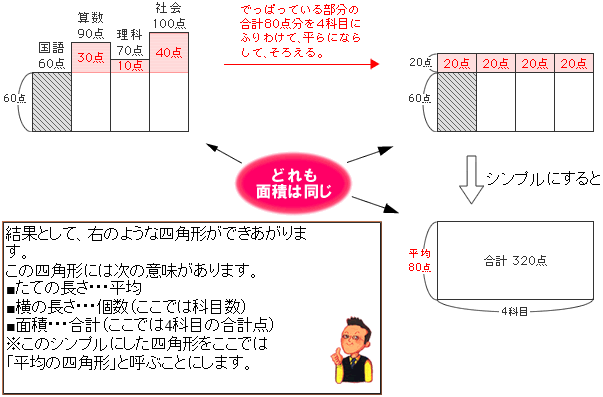
「平均」の2つの見方
①計算的な見方･･･「たしてわるのが平均」という考え方
平均＝合計÷個数
②図形的な見方(面積図)･･･「ならして、そろえるのが平均」という考え方
四角形のたての長さ･･･平均
四角形の横の長さ･･･個数
四角形の面積･･･合計
問題1
太郎君は、算数のテストの結果を一覧にすることにしました。ところが、4回目のテストをなくしてしまい点数がわからなくなってしまいました。平均点は86点ということはわかっています。4回目のテストは何点だったでしょうか。
解法
普通は次のような解き方をします。
平均点は86点なので、5回目までの合計点は、86×5＝430点
一方、4回目を除いた合計点は、96＋100＋86＋100＝382点
その差は、430－382＝48点
これが、4回目の点数です。
まとめると、平均を86点にするためには、5回の合計が430点である必要があり、そのためには、4回目の点数は48点でなければならないわけです。
平均は合計÷個数なので、逆に430÷5＝86点
ということも意識してください。
この問題に関しては以上の解き方がベストです。ただし、第2問以降で応用問題を解くために、もう一つの考え方をもう一度簡単に説明しておきます。もう一つの考え方とは図形的な見方、つまり「ならして、そろえるのが平均」という考え方です。
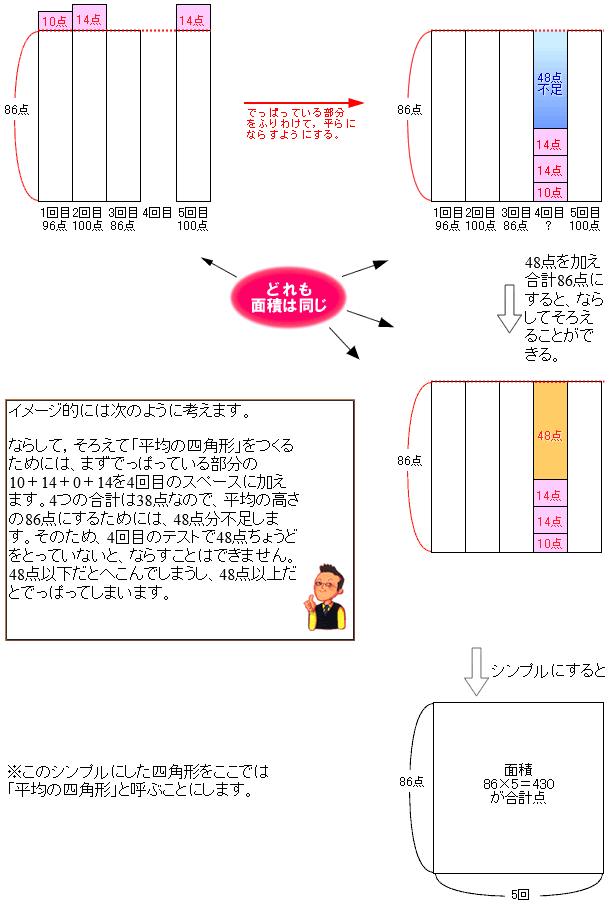
答え：48点
問題2
生徒数が４０人の組の国語のテストの平均点は63.1点でした。このうち男子の平均点は62点、女子の平均点は64点でした。この組の女子の人数は何人ですか。
解法
いよいよ平均算の応用問題です。まずは問題文にしたがって面積図（平均の四角形）を書いてみます。少し複雑ですが、図をよく見て考えてみてください。
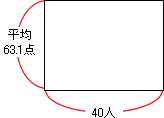
①40人の組の国語のテストの平均点は63.1点でした。
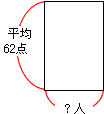
②男子の平均点は62点
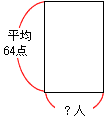
③女子の平均点は64点
ここで、面積図（平均の四角形）の面積はそれぞれの合計点を表しています。①の図の四角形の面積が全体の合計点になるので、クラス全体の合計点は63.1×40＝2524点です。
男子の合計点、女子の合計点は、男子・女子それぞれの人数（面積図の底辺の長さ）がわかっていないので求めることができません。
でも、男子の合計点と女子の合計点の和は全体の合計点と等しくなるので、②と③の面積をたしたものは①の面積(2524)と等しくなるはずです。
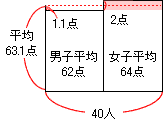
そこで、 ② と③の四角形をくっつけて次のような図で考えます。
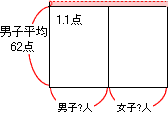
次に女子のでっぱっている部分
をならして、平らにします。
すると「全体の平均の四角形」ができます。
このようにして作った「全体の平均の四角形」は①の四角形と同じものになります。
ところで、ならすまえの女子のでっぱっている部分の面積 をならしたわけだから、
とならしたあとの面積 
は同じはずです。
ならした後の面積は 
なので，
1.1×40＝44となります。
ところで，もう一度，ならす前の四角形を見てみると
2点･･･女子の平均(64点)と男子の平均(62点)の差
つまり、 （女子？人）×２＝４４なので、（女子？人）＝４４÷２＝22人となり、これが正解です。
このように、平均算の応用問題は図を書き「ならして、そろえるのが平均」という考え方で解くことが原則です。問題を多く解き、面積図の書き方を覚え、ならす前とならした後の面積図のどの部分が同じになるかを見抜く力をつけることができれば、ばっちりです。
答え：22人
問題3
ある地区でボーリング大会の参加者を募集したところ、申込者の平均年齢は14才でした。ところが、直前になって11才、12才、14才、47才の4人が参加をとりやめました。結局、参加した人の平均年齢は12才になりました。最初に申し込みをした人は何人ですか。
解法
これも、平均算の応用問題です。かなり難しそうですが、とにかくできる範囲で面積図（平均の四角形）を書いてみましょう。
①最初の平均は１４才でした。
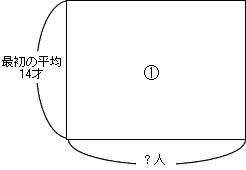
②４人抜けたら平均が１２才になりました。
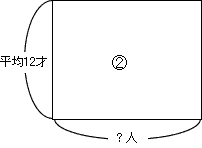
書けるものは，これだけでしょうか？ 実はまだ書けます。とりやめた4人の面積図（平均の四角形）です。
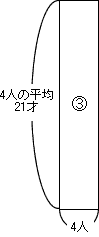
③やめた4人の年令の合計は，11＋12＋14＋47＝84才，平均は84÷4＝21才です。
繰り返しになりますが、平均の四角形の面積は合計を表しています。ここでは，参加者の年令の合計です。ということは，
①最初の平均の四角形は、②４人抜けたときの平均の四角形と③とりやめた4人の平均の四角形の和と等しくなるはずです。年令の合計は、全員いっしょのときも、二つに分けて、たしても変わらないからです。簡単に書くと
①の面積＝②の面積＋③の面積
となります。
面積図（平均の四角形）の面積は、合計を表しているから、
①最初の平均の四角形の面積②４人抜けたときの平均の四角形の面積③ とりやめた４人の平均の四角形の面積となります。
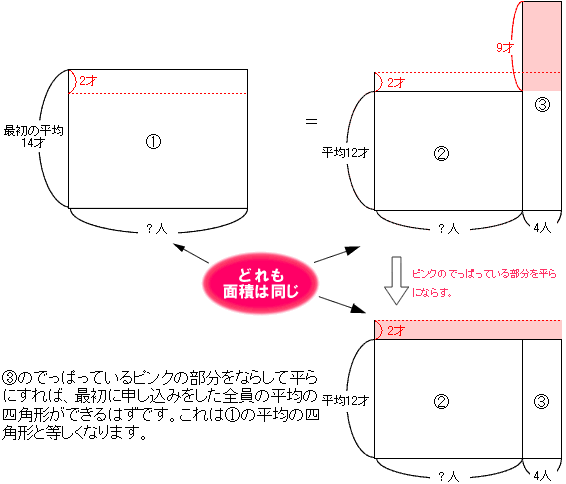
ピンクの部分に着目すると
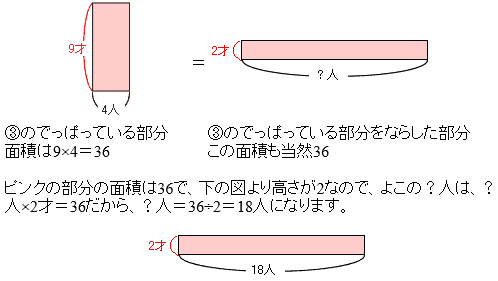
答え：18人
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
