学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
平均算（基礎編）
平均といえば、合計を個数で割って求めることは、よく知られていると思います。 たとえば、40点、80点、90点の3人の得点があるとき、 合計が40＋80＋90＝210点、個数が3だから、 210÷3＝70で、平均は70点となります。平均を求めたり、合計や個数などを求めたりする計算(問題)を平均算といいます。
平均算の問題では、平均について次の2つの見方を理解しておく必要があります。
①計算的な見方 ②図形的な見方（面積図）
具体的には問題を通して説明します。
特に今回は②の図形的な見方（面積図）を中心に説明します。これが理解できれば、多くの応用問題を解くことができます。
問題1
太郎君の4科目のテストの結果は、国語60点、算数90点、理科70点、社会100点でした。太郎君の4科目の平均点は何点ですか。
解法
4科目の合計は60＋90＋70＋100＝320点
平均は個数（科目数）で割って、320÷4＝80点
答え：80点
これが、「平均」の基本的な求め方です。この問題では、この解き方がベストです。
しかし応用問題になると、このように簡単な計算では求めることができません。そこで、図形的な見方（面積図）が登場します。
まず、4科目の得点をそれぞれ、次のように図（四角形）で表してみます。
それぞれの科目の四角形の高さが得点を表しています。
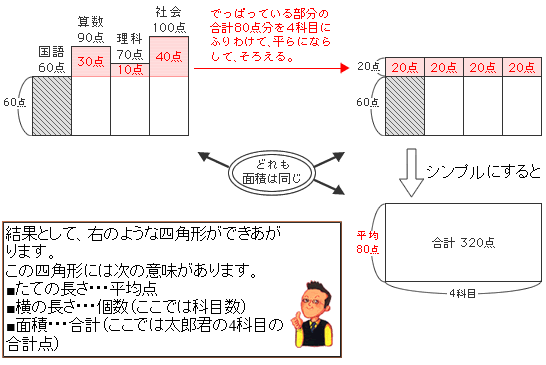
次に、一番得点の低い国語の60点を基準として、各科目の出ている部分に注目します。
このでっぱっている部分を4科目にふりわけて、平らになるようにならして、そろえます。
でっぱっている部分の合計は30＋10＋40＝80点なので、4科目にふりわけるとき、科目あたり20点ずつの配分になります。
左のピンクの部分の面積分を振り分けるので、どちらのピンクの部分も面積は同じです。全体の面積も同じです。 つまり、出っ張っている部分をうまく切り取って、平らにならすようなイメージです。
「平均」の2つの見方
①計算的な見方･･･「たしてわるのが平均」という考え方
平均＝合計÷個数
②図形的な見方(面積図)･･･「ならして、そろえるのが平均」という考え方
四角形のたての長さ･･･平均
四角形の横の長さ･･･個数
四角形の面積･･･合計
問題2
A君、B君、C君の3人の身長を比べたところ、B君はA君よりも3cｍ高く、A君はC君より9cｍ高かったそうです。A君の身長は、3人の身長の平均より何cｍ高いですか。
解法
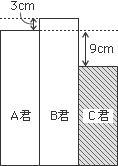
①問題文より、3人の身長の差を読み取って図に表すと次のようになります。
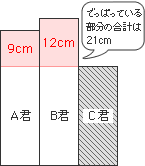
②次に一番身長の低いC君を基準として、でっぱっている部分に注目します。
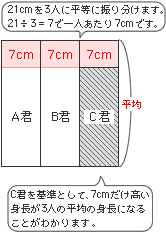
③でっぱっている部分の合計21cｍを3人にふりわけて、平らにします。この四角形の高さが平均です。
③の図より、C君を基準として、7cｍだけ高い身長が3人の平均になることがわかります。
すると、A君はC君より9cｍ高いから、A君は平均より2cm高いこともわかります。
（よくわからない人は下の図で考えてみてください）
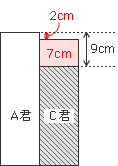
よくわからない場合は、自分で図を書いて考えるとわかると思います。
問題を解くときは必ず図を書いて考えることが大切です。
答え：2cm
問題3
A、B、C3人の身長の平均は131.5cｍ、D、Eの平均は135cｍです。このとき5人の身長の平均は何cｍですか。
解法
問題文を図にするとこのようになります。
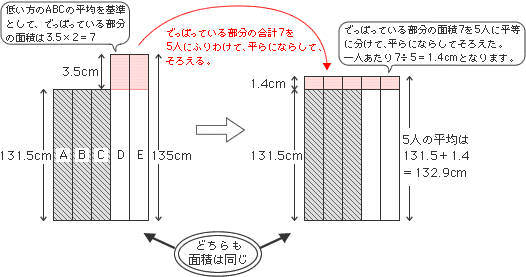
平均算を図形的な見方(面積図)で解く場合、1個1個の四角形の横の長さは1として、面積を計算します。
答え：132.9cm
今回はここまでにします。
平均を四角形の面積を利用して解くので、慣れるまで練習が必要かもしれませんが、この面積図の考え方を覚えてしまうと、平均算の応用問題を簡単に解くことができます。
次回は、応用問題にチャレンジしますので、それまでによく理解しておいてくださいね。
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
