ニュートン算(発展編)

前回のニュートン算の解きかたを基本として、今回は発展問題を解いてみます。難しい分野ですが、根気強く読んでいただければ、理解していただけると思います。理解できたら、さまざまな問題にもチャレンジしてみてください。 教え上手:きんたろう先生 (イラスト:たかまひびき)
ニュートン算の解法のポイント
ニュートン算は、ある量が一方では増え、また一方では減っていくような状況の中での問題なので、次の4つの量を求めることが解法のポイントになります。
①最初の量
②一定の時間に増える量
③一定の時間減る量
④実質的に減る量(③と②の差)
※一定の時間とは、1分、1時間、1日などです
これらは計算しなくても問題文に書かれていることもあります。そして、これらがわかったらイメージ図を描いて考えます。
今回の解法はこの4つの量を常に意識しながら読んでみてください。
なぜ、4つの量が必要なのかは、前回の内容を確認してください。
このポイントをもとにして、今回は前回の類題から解いてみます。
問題1(前回の復習問題)
ある劇場の前に120人の客が1列にならんで入場を待っています。さらに毎分20人の割合で客がその列に加わっていきます。いま、この劇場の1つの入り口から客を劇場の中に入れると、列がなくなるまでには12分かかります。はじめから2つの入り口から客を入れると列がなくなるまでには何分かかりますか。
解説
まず、問題を解くために必要な4つの量を確認します。

③と④が問題文には直接書いていないので、計算で求めます。
まず、③を求めます。
入り口が1つのとき、列がなくなるまで、何人の人が劇場の中に入ったかを計算して、12(分)でわれば、毎分、列からいなくなる人数(=毎分、劇場に入る人の数)がわかります。

劇場に入った人の合計人数を、かかった時間(分)でわれば、毎分何人が劇場に入ったかがわかります。
ここでは、
列からいなくなった人=劇場に入った人
という考え方をします。
列から何人の人がいなくなったかを計算します。
もともと、120人がならんでいました。
毎分(1分間につき)20人ずつ増えていきますが、列がなくなるまでには12分かかると書いてあります。
だから、12分間増え続け、列に加わった人数(増えた人数)は20×12=240人となります。

1分間で20人、12分では×12で、240人です。


もともと120人いて、240人が加わったのだから、合計で360人です。この360人がなくなった列の人数(劇場に入った人数)です。
ところで、1つ入り口からは、毎分(1分間につき)何人が劇場に入ったことになるのでしょうか?
12分で360人が劇場に入ったので、毎分(1分間につき)、360÷12=30人です。
これで、③の一定時間に減る量(毎分、列からいなくなる人の数。つまり、毎分、劇場に入る人の数)がわかりました。
その結果④の実質的に減る量(②と③の差)もわかります。ここで4つの量を確認します。

入り口が1つの場合、毎分(1分間につき)、30人が劇場に入ることができるわけです。 イメージを図に描くと次の通りです。

まとめると、矢印が打ち消しあって、次のような図になります。

次に、窓口が2つになった場合はどうでしょうか?
イメージ図は次のようになります。入り口が2つになったので、列から出て行く人は60人になります。

列から出て行く人は毎分合計60人、列に加わる人は毎分20人なので、まとめると、矢印が打ち消しあって、次のようになります。

最初に120人いて、毎分40人ずつ減ることになるので、列がなくなるまでには、
120÷40=3
で、3分かかることになります。
答え:3分
次は発展問題です。
問題2
ある牧場に、40頭の牛ではちょうど8日で食べつくし、70頭の牛では4日で食べつくすだけの牧草が生えています。この牧場に牛を50頭放牧すると、何日で牧草を食べつくしますか。ただし、1日あたりに牛1頭が食べる草の量と、1日あたりに生える草の量は、それぞれ一定であるとします。
解説
まず、4つの量を確認してみます。

どれも問題文に書かれていません。不明のまま図を書くと次のようになります。

これらのわからない数を求めるためには、普通は、線分図というものを書いて求めますが、ここでは、まずイメージとして、直観的に理解していただくため、図で説明します。
まず、問題文に書かれている内容をイメージ図で表すと次のようになります。


4つの数すべてが、不明なので、何の手がかりもありません。そこで「1頭の牛が1日に食べる草の量を1」としてみます。これが4つの数を求めるかぎ、つまり問題を解くかぎとなります。ニュートン算の問題の重要な解法テクニックです。 次の図のステップ①~ステップ⑤の順にみてください。




ここまでわかると、必要な量が次々に出てきます。図に数を入れてみます。


ここで4つの量を確認してみます。図より

4つの量がわかれば、いつもの図も書くことができます。50頭の牛で考えます。


最初の草の量は240で、実質的に減る草の量は1日につき40だから、
240÷40=6
となり、(50頭の牛では)6日間で食べつくすことになります。
答え:6日間
補足
4つの量を求めるときに、図で表しましたが、線分図を使って、簡単に表すと次のようになります。
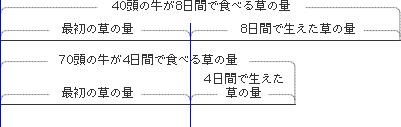
「1頭の牛が1日に食べる草の量を1」とすると、 の量がわかり、それをもとに、
の量がわかり、それをもとに、 の量がわかります。
の量がわかります。
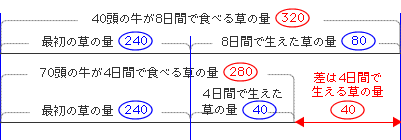

(牧場に生える草の量は牛が何頭いても同じだから) 差の40は4日間に生える草の量となり、1日に生える量は、4でわって、10となります。 その結果4日間では40の草が生え、8日間では、 80の草が生えることになります。

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
関連記事
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
