2004.02.10

ニュートン算（基礎編）

ニュートン算はリンゴが落ちるのを見て引力を発見したニュートンが考えた問題だから、このような名前が付けられていると言われています。

ニュートン算の解法のポイント

ニュートン算は、ある量が一方では増え、また一方では減っていくような状況の中での問題なので、次の4つの量を求めることが解法のポイントになります。
①最初の量
　　②一定の時間に増える量
　　③一定の時間減る量
④実質的に減る量（③と②の差）
※一定の時間とは、1分、1時間、1日などです

これらは計算しなくても問題文に書かれていることもあります。そして、これらがわかったらイメージ図を描いて考えます。
今回の解法はこの4つの量を常に意識しながら読んでみてください。

問題1

太郎君は今100円持っています。今日から太郎君は毎日10円のおこづかいがもらえますが、毎日30円を使います。太郎君の持っているお金は何日目でなくなりますか（今日を1日目とします）。

解説

ニュートン算の基本問題です。おこづかいを毎日10円ずつもらうのでお金が増えますが、一方では、毎日30円ずつ使うので減っていきます。減るほう(使うほう)が多いので、いつかはなくなります。
毎日のお金の減り方を表にして調べてみましょう。最初に持っているお金は100円です。

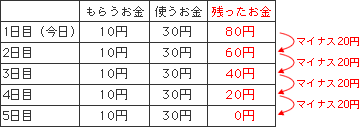
残ったお金を見ると、毎日20円ずつ減っていることがわかります。
もらう(増える)お金が10円、使う(減る)お金が30円なので、
実質的には差し引き20円が減ることになるからです。
そして5日目で、お金がなくなります。

①最初の量は100円
②一定の時間に増える量は10円
③一定の時間減る量は30円
です。これをイメージ図にします。
※一定の時間は、ここでは1日間のことです

これをイメージ図に書いてみます。

上の図と下の図は、同じことを意味しています。ニュートン算では、下の図を書いて、問題を考えると簡単です。
もともと100円あって、実質的には毎日20円ずつ減っていくのですから、
100÷20＝5
5日目でお金がなくなることがわかります。

実質的には、差し引き20円が減るので（矢印が打ち消しあって）、次のような図になります。

この図は、最初に100円持っていて、実質的には毎日20円ずつ減っていくのですから、
100÷20＝5
5日目でお金がなくなることが計算できます。

ニュートン算の問題解法の基本的な流れは次の通りです。
①最初の量を求める（ここでは100円）
②一定の時間に増える量を求める（ここでは10円）
③一定の時間に減る量を求める（ここでは30円）
④ ③と②の差（実質的に減る量）で、①を割るとなくなるまでの時間（答え）がでる。
最初の量÷（一定の時間に減る量－一定の時間に増える量）
ここでは、100÷（30－10）＝5日　となります。

答え：5日目

問題2

ある野球の試合で前売券を発売しはじめたとき、窓口にはすでに、720人がならんでいました。さらに、毎分12人の割合でこのならんでいる行列に人が加わっています。窓口が1つのときには、40分で行列がなくなります。窓口が2つあると、何分で行列はなくなりますか。

解説

問題1では、太郎君のさいふのお金の増減で考えましたが、ここでは行列の人の増減で考えます。
まず、問題文より、最初の量は720人。一定の時間(ここでは1分間)で増える量、つまり行列に加わる人の数は、毎分12人です。
減る量は行列にならんでいた人が窓口で前売券を買って、行列から出て行く人数です。
これは、問題文には書かれていないので、自分で計算してみましょう。

どうすれば、求めることができるのでしょうか。
それは、行列がなくなるまでに何人の人が何分で前売券を買ったかを計算します。そして毎分何人かを計算すればよいわけです。
そのためまず、窓口が一つのとき、行列がなくなるまでに（40分間に）、何人の人に前売券を売ったのかを計算します。

もともと、720人がならんでいました。毎分(1分間につき)12人が加わりましたが、40分で行列がなくなったと書いてあります。
だから、行列がなくなるまでに、新たに行列に加わった人数は12×40＝480人となります。

1分間で12人、40分間では×40で、480人です。

もともとの720人いて、480人が加わったのだから、合計で1200人です。この1200人がなくなった行列の人数（1つの窓口で40分間に前売券を買った全員の人数）です。

ところで、この窓口では、毎分(1分間につき)何人に販売したことになるのでしょうか？
40分で1200人に販売したので、毎分(1分間につき)、1200÷40＝30人です。

720人の行列が40分でなくなったから、720÷40＝18で、毎分18人とするのは「まちがい」ですよ。なぜなら、その40分の間にも、毎分12人ずつ増えているからです。

つまり、窓口が1つの場合、毎分(1分間につき)、30人に販売することができるわけです。
言いかえると、減る量は1分間に30人です。
窓口が2つになれば60人、3つになれば90人・・・です。

窓口の担当者のすばやさは1分間に30人ということになります。

イメージを図に描くと次の通りです。

実質的には差し引き18人が減るので（矢印が打ち消しあって）、次のような図になります。

次に、窓口が2つになった場合はどうでしょうか？
イメージ図は次のようになります。

行列の人数に注目すると、最初に720人いて、実質的には毎分48人ずつ減ることになるので、
行列がなくなるまでには、
720÷48＝15
で、15分かかることになります。

かなり、丁寧に説明したつもりですが、ニュートン算はやはり理解しづらい問題だと思います。よくわからない場合は、とりあえず、問題1と問題2で説明した解き方(考え方)を定石として、同じような問題を多く解くことにより、理解を深めていきましょう。

答え：15分

問題3

遊園地の入場券売り場に120人並んでいます。行列は毎分6人の割合で増えていきます。1つの窓口で売り始めたら20分で行列はなくなりました。はじめから窓口を3つにして売ったら、何分で行列はなくなりますか。

解説

まず、問題文より、最初の量は120人、一定の時間(ここでは1分間)で増える量、つまり行列に加わる人の数は、毎分6人です。
減る量は行列にならんでいた人が窓口で入場券を買って、行列から出て行く人数です。
これは、問題文には書かれていないので、自分で計算してみましょう。
問題2と同じように、行列がなくなるまで（20分間）に、入場券を買った人数を計算して、毎分何人が行列から出て行ったかを計算します。

もともと、120人がならんでいました。毎分(1分間につき)6人ずつ増えていきますが、20分で行列がなくなったと書いてあります。
だから、行列に加わった人数（増えた人数）は6×20＝120人となります。

1分間で6人、20分間では×20で、120人です。

もともとの120人いて、120人が加わったのだから、合計で240人です。この240人がなくなった行列の人数（1つの窓口で20分間に入場券を買った全員の人数）です。

ところで、この窓口では、毎分(1分間につき)何人に販売したことになるのでしょうか？
20分で240人に販売したので、毎分(1分間につき)、240÷20＝12人です。
つまり、窓口が1つの場合、毎分(1分間につき)、12人に販売することができるわけです。
言いかえると減る量は1分間に12人です。
窓口が2つになれば24人、3つになれば36人・・・です

イメージを図に描くと次の通りです。

実質的には差し引き6人が減るので（矢印が打ち消しあって）、次のようになります。

上の図と下の図は同じことを意味しています。

次に、窓口が3つになった場合はどうでしょうか？
イメージ図は次のようになります。

行列から出て行く人は合計36人、行列に加わる人は6人なので、
実質的には差し引き30人が減るので（矢印が打ち消しあって）、
次のようになります。

最初に120人いて、実質的には毎分30人ずつ減ることになるので、
行列がなくなるまでには、
120÷30＝4
で、4分かかることになります。

答え：4分

教え上手きんたろう先生

「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。

発展編を読む