通過算（発展編）

　長さ210ｍ、秒速32ｍのＡ列車と長さ140ｍ、秒速18ｍのＢ列車がすれ違うとき、出会ってから離れるまでに何秒かかりますか。

解法を見る


Ａ列車が秒速15ｍの速さで進行しています。そこへ、秒速22ｍの速さで進んできた長さ75ｍのＢ列車が追い越しました。追い越しにかかった時間は24秒でした。Ａ列車の長さは何ｍになりますか

解法を見る


15両編成の急行列車がある駅のホームで立っている1人の人の前を6秒で通過しました。また、ホームを通過するのに13秒かかりました。しばらくして、この急行列車は、同じ方向へ向かう９両編成で、秒速14ｍの普通列車に追いつき、追い越していきました。列車の1両はいずれも8ｍです。
（１）急行列車の速さは秒速何ｍですか。
（２）ホームの長さは何ｍですか。
（３）急行列車が普通列車に追いてから、追い越すまでに何秒かかりましたか。

解法を見る

今回は前回の続きです。前回説明した通り、通過算のいちばんの解法ポイントは列車が進む距離（道のり）を求めることです。今回は詳しく説明しませんが、必ず確認の上、今回の内容を読んでください。速さの意味については、もう一度ここで説明します。

（再掲載）
速さは「秒速」「分速」「時速」等で表します。

	秒速・・・	１秒間に進む距離を表します（例えば、秒速5ｍとは1秒間に5ｍ進む速さのこと）。
	分速・・・	１分間に進む距離を表します（例えば、分速300ｍとは1分間に300ｍ進む速さのこと）。
	時速・・・	１時間に進む距離を表します（例えば、時速180kmとは１時間に180km進む速さのこと）。

秒速5ｍは1秒間に5ｍ進む速さなので、1分間（60秒）では、その60倍進むことになるので、5×60＝300ｍ進むことになります。つまり、分速300ｍです。結局、秒速5ｍと分速300ｍは同じ速さなのです（秒速5ｍ＝分速300ｍ）。

※算数では、基本的に速さを「秒速」と「時速」で表します。そして、秒速にはｍを使い、秒速3ｍのように表し、時速ではkmを使い、時速100kmのように表します。ちなみに、よくみかける自動車のスピードメーターに用いられている〔km/h〕は時速のことです。

今回は列車がすれちがったり、追い越したりする場合の問題を解きます。話の中心は、自分が電車に乗って進行しているとき、自分の電車に近づいたり、遠ざかったりする別の電車を見たときの速さです。通過算で列車がすれちがったり、追い越したりする問題は、自分の電車が本当は動いているのだけども止めて考えるという独特な方法で解きます。とてもイメージがわきにくいところです。まずは文章で説明します。

●動く景色
皆さんが電車に乗って、窓から景色を眺めると、景色が次々に変わっていきます（景色が動いて見えます）。ゆっくり電車が動いているときは、景色もゆっくり動き、電車が速く動いているときは景色も速く動きます。そして、電車が止まっているときは、景色は止まっています。
ところで、動いているものには、必ず速さがあります。景色はどのくらいの速さで動いているのでしょうか？もし、皆さんが、秒速10ｍの速さの電車に乗っているときは、景色は秒速10ｍの速さで動いてみえます。秒速25ｍの速さの電車に乗っているときは、景色は秒速25ｍの速さで動いてみえます。ここで、重要なことは実際には景色は地面に固定されているので、静止しているということです。つまり、動いているのは景色ではなく、電車に乗っている自分であるということです。景色が動くという考え方は、言いかえると、自分は電車に乗って動いているにも関わらず、自分は止まっているという考え方をしていることになります。この本当は動いているのだけども自分を止めて考える方法は、通過算の発展問題（特に追い越しとすれ違いの問題）を解く上でのポイントになります。

●列車のすれ違い
皆さんが秒速25ｍの速さの電車に乗っているときを考えましょう。先頭の運転席の隣で、前方を見ているところをイメージしてみてください。今、となりの線路の前方に電車が止まっています。本当は動いているのだけども自分を止めて考えると、前方の電車は近づいてくるように見えます。近づいてくる速さは秒速25ｍです。
それでは、前方の電車が秒速5ｍでゆっくりとこちらに向かってきている場合はどうでしょうか？止まっているときと比べて、少し速く近づいてくるように見えます。先の場合とくらべて、さらに秒速5ｍの速さだけ速く、秒速30ｍで近づいてくるように見えます。そして、いつかすれ違って後方に去っていきます。去っていくときの速さも近づいてくるときと同じで秒速30ｍです。
結論はすれちがうときの速さは２つの列車の速さの和になります。イメージがわかない人はこの結論だけは覚えてください。

●列車の追い越し
今度は皆さんの乗っている電車が停止しました。そこへ隣の線路の後方から秒速20ｍの速さの電車が近づいてきました。皆さんは本当に止まっているわけですから、後方の電車は秒速20ｍの速さで近づいてくるように見えます。それでは、皆さんの乗っている電車が秒速5ｍの速さで前方に動き出した場合はどうでしょうか？後方から近づいてくる秒速20ｍの電車の近づき方は、速くなるでしょうか、遅くなるでしょうか？イメージするのが、少し難しいと思います。後方の電車は秒速20ｍ（1秒間に20ｍ）で近づくのですが、同時に皆さんは秒速5ｍ（1秒間に5ｍ）で後方の電車から離れていることになります。そのため、皆さんからみると、後方の電車の近づきかたは止まっているときと比べて秒速5ｍの速さ分だけ遅くなって、秒速15ｍで近づいてくるように見えます。そして、いつか追い越して前方に去っていきます。去っていくときの速さも近づいてくるときと同じで秒速15ｍです。
結論は追い越すときの速さは２つの列車の速さの差になります。イメージがわかない人はこの結論だけは覚えてください。

---

長さ210ｍ、秒速32ｍのＡ列車と長さ140ｍ、秒速18ｍのＢ列車がすれ違うとき、出会ってから離れるまでに何秒かかりますか。

■ 解法
Ａ列車に乗って考えます。自分（Ａ列車）が止まっていると考えると、Ｂ列車は32＋18（＝２つの列車の速さの和）で秒速50ｍで近づいてくるように見えます。
前回と同様に下図の先頭の赤い印に注目して、出会ってから、離れるまでのＢ列車の移動した距離を求めると、350ｍになります（このとき、Ａ列車は止まっていると考えます）。





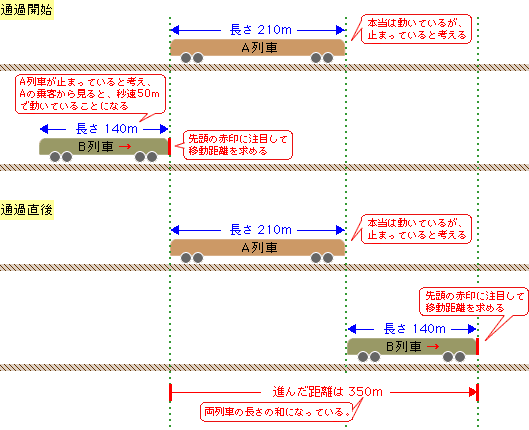
結局、Ｂ列車は、秒速50ｍ（1秒間に50ｍ動く速さ）で、350ｍの距離を移動することになるので、出会ってから、離れるまでに350÷50＝7秒かかることになります。


■ 答え：7秒

---

Ａ列車が秒速15ｍの速さで進行しています。そこへ、秒速22ｍの速さで進んできた長さ75ｍのＢ列車が追い越しました。追い越しにかかった時間は24秒でした。Ａ列車の長さは何ｍになりますか。

■ 解法
Ａ列車に乗って考えます。自分（Ａ列車）が止まっていると考えると、Ｂ列車は22－15（＝２つの列車の速さの差）で、秒速7ｍで近づいてくるように見えます。



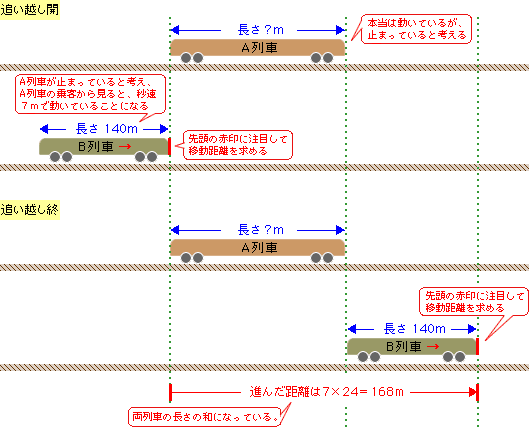
Ｂ列車は秒速７ｍ（1秒間に７ｍ）でＡ列車を24秒かけて、追い越すので、追い越す間に進んだ距離は、7×24＝168ｍです。これは上の図よりＡ列車とＢ列車の長さの和になるので（先頭の赤い印に注目）、Ａ列車の長さは、168－75＝93ｍとなります。

■ 答え：93ｍ

※列車がすれちがったり、追い越したりするときの進む距離（道のり）は両列車の長さの和になっていることを問題１、問題２で再確認してください。

---

最後に通過算の総まとめの問題を解いてみましょう。まずは、自力でチャレンジしてみてください。


15両編成の急行列車がある駅のホームで立っている1人の人の前を6秒で通過しました。また、ホームを通過するのに13秒かかりました。しばらくして、この急行列車は、同じ方向へ向かう９両編成で、秒速14ｍの普通列車に追いつき、追い越していきました。列車の1両はいずれも8ｍです。
（１）急行列車の速さは秒速何ｍですか。
（２）ホームの長さは何ｍですか。
（３）急行列車が普通列車に追いてから、追い越すまでに何秒かかりましたか。

■ 解法
まずは、急行列車と普通列車の長さを間違いのないように計算することが前提になります。1両が8ｍなので、
急行列車は15×8＝120ｍ、普通列車は9×8＝72ｍとなります。

（１）前回の問題１（ふみきりで立っている人の前を列車が通過する問題）と同様に解くことができます。速さを求めるためには、どれだけの時間にどれだけの距離を進んだかを問題文から読み取ります。



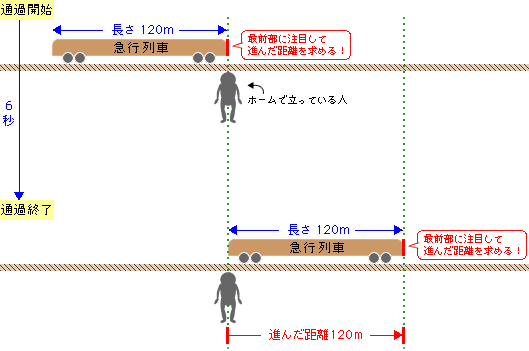
まず、通過するのにかかった時間は6秒。進んだ距離はこれまでと同様に、列車の最前部に注目すると、列車の長さと等しくなるので120ｍです。
　結局、6秒で120ｍの距離を進んだわけですから、1秒では、120÷6＝20ｍ進んだことになります。秒速は1秒間に進む距離ですから、この急行列車は秒速20ｍということになります。

■（１）答え：秒速20ｍ

（２）前回の問題２（鉄橋を渡る問題）や問題３（トンネルを抜ける問題）と同じように解くことができます。



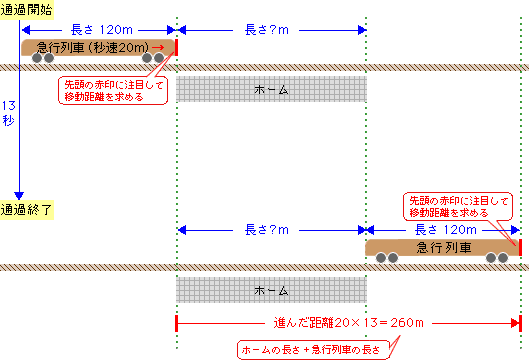
列車は、ホームを通過するのに、秒速20ｍで13秒（1秒間に20ｍ進む速さで13秒）かかったので、
20×13＝260ｍ進んだことになります。
このホームを通過するために進んだ距離（260ｍ）は上図より〔ホームの長さ〕＋〔急行列車の長さ〕なので、進んだ距離（260ｍ）から、急行列車の長さ（120ｍ）を引けば、ホームの長さが求められます。
したがって、ホームの長さは、260－120＝140ｍとなります。

■（２）答え：140ｍ

（３）今回の問題２と同様に解くことができます。普通列車に乗って考えます。自分（普通列車）が止まっていると考えると、急行列車は20－14＝6（＝２つの列車の速さの差）で、秒速6ｍで近づいてくるように見えます。



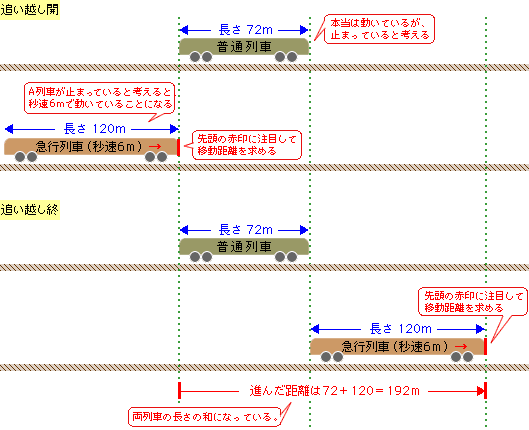
上の図より、急行列車は秒速6ｍ（1秒間に6ｍ動く速さ）で、普通列車に追いてから、追い越すまでに192ｍ進むことになるので、かかる時間は192÷6＝32秒となります。

■（3）答え：32秒

このページのTOPへ▲