通過算（基礎編）

長さ180ｍの列車が、ふみきりで立っている人の前を通過するのに6秒かかりました。
この列車の秒速は何ｍですか。

解法を見る


長さ150ｍの列車が秒速40ｍの速さで進んでいます。
この列車が長さ250ｍの鉄橋を渡りはじめました。渡り終わるまでに何秒かかりますか。

解法を見る


　秒速25ｍの列車が長さ1220ｍのトンネルを抜けるのに、52秒かかりました。
列車の長さは何ｍですか。

解法を見る

　通過算のメインキャストは「列車」です。列車が登場するほとんどの問題は「通過算」です。通過算は、列車がトンネルや鉄橋などを通過するときの速さや時間、距離などを求める問題です。通過算の応用問題は数多くありますが、今回は応用問題を解くための通過算の基礎について説明します。
　通過算のいちばんの解法ポイントは列車が進む距離（道のり）を求めることです。この列車が進む距離（道のり）に注意しながら、読んでみてください。

　問題を解く前に速さの意味について確認します。速さは「秒速」「分速」「時速」等で表します。

	秒速…	１秒間に進む距離を表します （例えば、秒速5ｍとは1秒間に5ｍ進む速さのこと）。
	分速…	１分間に進む距離を表します （例えば、分速300ｍとは1分間に300ｍ進む速さのこと）。
	時速…	１時間に進む距離を表します （例えば、時速180kmとは１時間に180km進む速さのこと）。

秒速5ｍは1秒間に5ｍ進む速さなので、1分間（60秒）では、その60倍進むことになるので、5×60＝300ｍ進むことになります。つまり、分速300ｍです。結局、秒速5ｍと分速300ｍは同じ速さなのです（秒速5ｍ＝分速300ｍ）。

※算数では、基本的に速さを「秒速」と「時速」で表します。そして、秒速にはｍを使い、秒速3ｍのように表し、時速ではkmを使い、時速100kmのように表します。ちなみに、よくみかける自動車のスピードメーターに用いられている〔km/h〕は時速のことです。

---

長さ180ｍの列車が、ふみきりで立っている人の前を通過するのに6秒かかりました。
この列車の秒速は何ｍですか。

■ 解法
　速さを求めるためには、どれだけの時間にどれだけの距離を進んだかを問題文から読み取る必要があります。この問題文の状況を図にすると次のようになります。この図から何秒間にどれだけの距離を進んだのかがわかりますか？


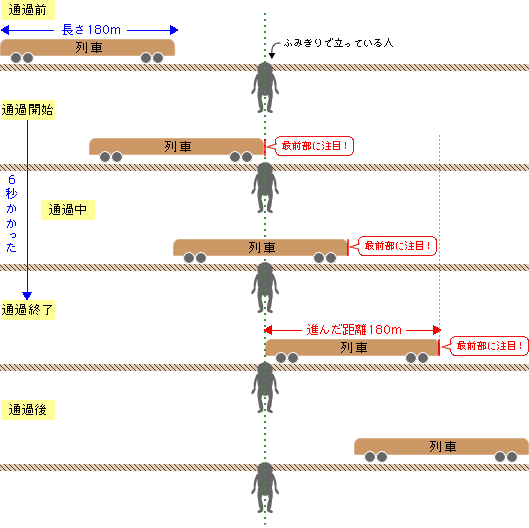
図より、6秒で180ｍの距離を進んだことがわかります。

わからない人は次のように考えてみましょう。

●通過にかかった時間
通過開始から通過終了までに6秒かかります。これは、問題文に「ふみきりで立っている人の前を通過するのに6秒かかりました」とあるからです。

●進んだ距離
進んだ距離は列車の最前部に注目して考えるとよいでしょう。図では赤い線をつけておきましたが、赤い線は通過開始から通過終了まで、180ｍ進むことになります（ここでは、列車の長さと等しくなります）。
結局、6秒で180ｍの距離を進んだわけですから、1秒では、180÷6＝30ｍ進んだことになります。秒速は1秒間に進む距離ですから、この列車は秒速30ｍということになります。

■ 答え：秒速30ｍ

進んだ距離を求めるときは、列車のどこか一部がどれだけ進んだかで考えます。この問題１のように最前部の移動した距離で考えてもよいし、列車の最後部でも真ん中でも求めることができます。ただし、最前部が一番わかりやすいのでここでは最前部で進んだ距離を求めることにします。
問題１では、6秒で180ｍの距離を進んだことより、1秒では、180÷6＝30ｍ進んだことになり、秒速30ｍと答えが出ましたが、
速さは〔進んだ距離〕÷〔かかった時間〕で求めることができるのです。

---

長さ150ｍの列車が秒速40ｍの速さで進んでいます。
この列車が長さ250ｍの鉄橋を渡りはじめました。渡り終わるまでに何秒かかりますか。

■ 解法
まず、どれだけの距離を進んだのかを考えてみましょう。鉄橋の長さが250ｍだから進んだ距離は250ｍと早合点しないでくださいね。下のように図で表すとわかると思います。図の最前部の赤い印に注目してください。



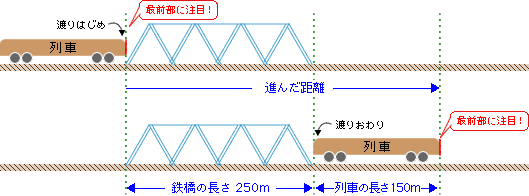
列車が鉄橋を渡りはじめてから、わたりおわるまでに進んだ距離（＝列車の最前部が進む距離）は
〔鉄橋の長さ〕＋〔列車の長さ〕になっていることがわかります。つまり、列車が鉄橋を渡りきるためには、列車自身も渡り切らなければならないので、鉄橋の長さに列車の長さを加えた距離を進まなければならないのです。結局、列車が進んだ距離は250＋150＝400ｍです。

※先に説明したように最後部に注目して、列車が鉄橋を渡りはじめてから、わたりおわるまでに進んだ距離を求めることもできます。

ところで、この列車は秒速40ｍですから、1秒間に40ｍ進みます。400ｍ進むためには、400÷40＝10秒かかることが計算できます。

■ 答え：10秒

鉄橋やトンネルを通過するとき、列車が進んだ距離は
〔鉄橋やトンネルの長さ〕＋〔列車の長さ〕となります。
問題２では、秒速40ｍで400ｍ進むのにかかる時間を400÷40＝10秒と求めましたが、かかった時間は〔進んだ距離〕÷〔速さ〕で求めることができるのです。

---

秒速25ｍの列車が長さ1220ｍのトンネルを抜けるのに、52秒かかりました。
列車の長さは何ｍですか。

■ 解法
これまでと同様に進んだ距離から求めてみましょう。




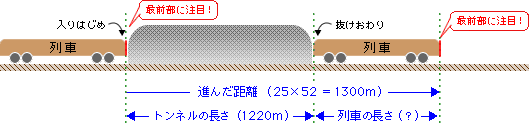
列車は、トンネルを抜けるのに、秒速25ｍで52秒（1秒間に25ｍ進む速さで52秒）かかったので、
25×52＝1300ｍ進んだことになります。
このトンネルを抜けるために進んだ距離（1300ｍ）は鉄橋の時と同じように、〔トンネルの長さ〕＋〔列車の長さ〕なので、進んだ距離（1300ｍ）から、トンネルの長さ（1220ｍ）を引けば、列車の長さが求められます。
したがって、列車の長さは、1300－1220＝80ｍとなります。

■ 答え：80ｍ

通過算の解法のポイント１：「列車が進む距離（道のり）を求めること」
…図に表して、列車の最前部に着目して求める。

	・ある地点を通過するとき（→問題１） 　列車が進む距離（道のり）＝列車の長さ
	・鉄橋やトンネルを通過するとき（→問題２、問題３） 　列車が進む距離（道のり）＝〔鉄橋やトンネルの長さ〕＋〔列車の長さ〕

※速さは〔進んだ距離〕÷〔かかった時間〕で求め、かかった時間は〔進んだ距離〕÷〔速さ〕で求めることができることも説明しましたが、最初に説明した速さの意味（定義）をきちんと理解していれば、これらを公式として暗記する必要はありません。むしろ、速さの意味（定義）を理解しないまま公式としてそのまま使ってしまうと、単位などで間違う可能性もあり、融通が利かなくなります。「速さの意味（定義）から結果としてでてくる式」として理解しておくとよいでしょう。

上のポイントに書いた、列車が進む距離（道のり）を求める式についても、同様なことが言えます。