旅人算

　難易度★

太郎君は毎分55mで歩きます。弟の次郎君は毎分45mで歩きます。
（１）太郎君と次郎君が1km離れた位置から向かい合って進むとき、何分後に出会うことになりますか。
（２）太郎君は、次郎君の500m後から出発して次郎君を追いかけました。何分後に追いつきますか。
解法を見る

　難易度★★

お父さんは7時に家を出て毎分150mの速さで駅に向かいました。ところが忘れ物に気が付いたお父さんは家から3km行ったところで、ひき返しました。太郎君はお父さんが家を出てから12分後（7時12分）にお父さんが忘れ物をしたことに気が付いて毎分200mの速さでお父さんを追いかけました。太郎君は何時何分にお父さんに追いつくでしょうか。
解法を見る

　難易度★★★

これは、チャレンジ問題です。
１周1800mの池があります。この池のまわりを兄と弟がそれぞれ同時に同じ場所から反対方向に歩き始めると、15分後に2人は出会います。また、同時に同じ場所から同じ方向に歩き始めると、90分後に兄が弟を追い抜きます。兄と弟の歩く速さはそれぞれ分速何mですか。
解法を見る

---

太郎君は毎分55mで歩きます。弟の次郎君は毎分45mで歩きます。
（１）太郎君と次郎君が1km離れた位置から向かい合って進むとき、何分後に出会うことになりますか。
（２）太郎君は、次郎君の500m後から出発して次郎君を追いかけました。何分後に追いつきますか。

■ 解法
（１） まず、「毎分55m」とは、1分間に55m進む速さのことで、「分速55m」と表現するときもあります。 同様に、「毎時4km」の場合は1時間に4km進む速さのことで、「時速4km」と表現するときもあります。 　さて、問題ですが、いつもと同様にまず、図で説明します。




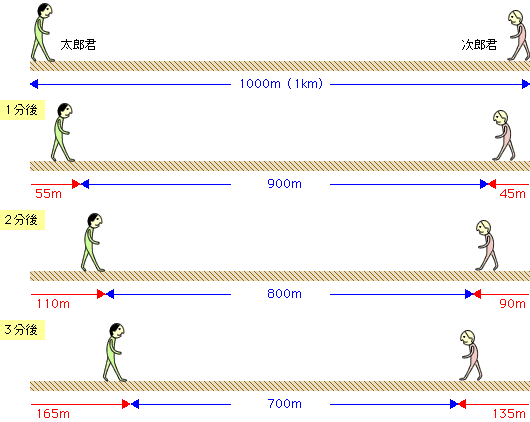
【１分後には】
太郎君は55m、次郎君は45mだけ進みますから、二人の距離は900mになります。
(＝1000－(55＋45))

【２分後には】
太郎君はさらに55m進んで、55＋55＝110m
(＝55×2)

次郎君はさらに45m進んで、45＋45＝90m
(＝45×2)

二人の距離は800mになります。
(＝1000－(110＋90))

【３分後には】
太郎君はさらに55m進んで、55＋55＋55＝165m
(＝55×3)

次郎君はさらに45m進んで、45＋45＋45＝135m
(＝45×3)

二人の距離は700mになります。
(＝1000－(165＋135))

ここで、重要なことは、二人の距離が1分間ごとに100mずつ近づいているということです。このことが分かれば、1000mの中に100mがいくつ分あるかということになり、1000÷100という式ができ、10分後に二人が出会うことがわかると思います。

一般的には次のように解きます。

<一般的な解法>
二人の歩く速さはそれぞれ毎分55m、毎分45mであるから、
1分間につき55＋45＝100mずつ近づいている。
二人の距離は最初1000m（1km）であったから、1000÷100＝10分

■ 答え
10分後


（２）
この問題も頭の中だけで考えようとすると混乱すると思うので、慣れるまでは図で考えていきましょう。





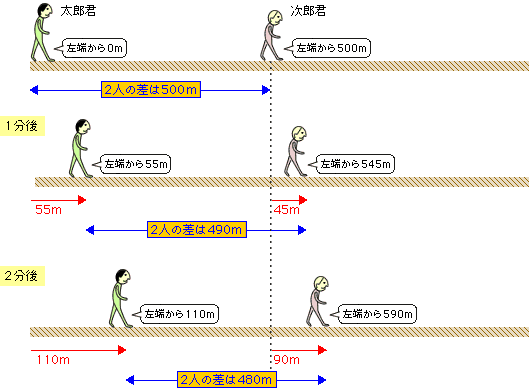
ここでも、二人の距離が1分間ごとに10mずつ近づいているというがポイントになります。（1）と同様に500mの中に10mがいくつ分あるかということになり、500÷10という式ができ、50分後に二人が出会うことがわかります。
　一般的には次のように解きます。

<一般的な解法>
二人の歩く速さはそれぞれ毎分55m、毎分45mであるから、
1分間につき55－45＝10mずつ近づいている。
二人の距離は最初500mであったから、500÷10＝50分

■ 答え
50分後

---

お父さんは7時に家を出て毎分150mの速さで駅に向かいました。ところが忘れ物に気が付いたお父さんは家から3km行ったところで、ひき返しました。太郎君はお父さんが家を出てから12分後（7時12分）にお父さんが忘れ物をしたことに気が付いて毎分200mの速さでお父さんを追いかけました。太郎君は何時何分にお父さんに追いつくでしょうか。

■ 解法
旅人算の応用問題です。この問題をこれまでと同様にして、
二人の近づく距離は150＋200で1分間に350mだから3000（3km）÷350などと考えては駄目ですよ。なぜかと言うと、お互いに3km離れた地点から二人が同時に近づき始めたとは限らないからです。お父さんが引き返した時刻は太郎君が家を出る前かも知れませんし、出た後かもしれないのです。少し難しい問題ですが、ゆっくり考えていきましょう。

まず、お父さんが何分後に引き返したかを求めてみましょう。
お父さんは毎分150mの速さなので、3km（＝3000m）進むためには、3000÷150＝20分かかります。
つまり、お父さんは7時20分に忘れ物に気がつき、ひき返したのです。
太郎君が家を出てから8分後です。
その間に太郎君は200×8＝1600mだけ家から進んでいることになります。



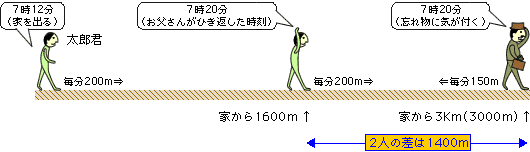
結局、7時20分には、お父さんは家から3000mの地点にいて、太郎君は家から1600mの地点にいることになります。その時点で二人の距離は3000－1600＝1400mです。

二人の近づく距離は150＋200で1分間に350mだから、1400÷350＝4でさらに（7時20分から）4分後にお父さんと太郎君は出会うことになります。つまり、正解は7時24分です。
　
■ 答え
7時24分

---

１周1800mの池があります。この池のまわりを兄と弟がそれぞれ同時に同じ場所から反対方向に歩き始めると、15分後に2人は出会います。また、同時に同じ場所から同じ方向に歩き始めると、90分後に兄が弟を追い抜きます。兄と弟の歩く速さはそれぞれ分速何mですか。

■ 解法
第1問、第2問より
2人がお互いに近づくとき・・・「二人の速さ（分速）の和」＝「二人が1分間に近づく距離」
一方が相手を追いかけるとき・・・「二人の速さ（分速）の差」＝「二人が1分間に近づく距離」
ということがおわかりいただけたと思います。このことを踏まえて第3問を考えてみましょう。

まず、
「兄と弟がそれぞれ同時に同じ場所から反対方向に歩き始めると、15分後に2人は出会う」ことより
最初は1800m離れていた二人が15分かけて出会ったことになるので、
1800mを15等分すると、1分間ごとに近づく距離＝「二人の速さ（分速）の和」を求めることができます。

「二人の速さ（分速）の和」＝1800÷15＝120

次に
「同時に同じ場所から同じ方向に歩き始めると、90分後に兄が弟を追い抜く」ことより
最初は1800m（1周）離れていたが、兄が90分かけて追いついたことになるので、
1800mを90等分すると、1分間ごとに近づく距離＝「二人の速さ（分速）の差」を求めることができます。
「二人の速さ（分速）の差」＝1800÷90＝20

和が120、差が20となる２つの数は、70と50であるから、兄は分速70m、弟は分速50mとなります。

※最後は通常「和差算」と呼ばれる計算で求めます。「和差算」とは二つの数の和と差がわかっているとき、
　和と差をたして、２で割ると大きい方の数が
　和から差を引いて、２で割ると小さい方の数が
出るというものです。
この問題の場合
（120＋20）÷2＝70　大きい方の数
（120－20）÷2＝50　小さい方の数
ということになります。

■ 答え
兄は分速70m、弟は50m