カレンダーの曜日を求める！

---

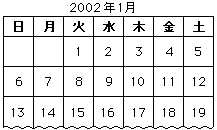
カレンダーの法則（きまり）をみつけてみよう。

右のカレンダーは2002年1月の第3週までのものです。
（１）2002年1月30日は何曜日になりますか。
（２）2002年2月24日は何曜日になりますか。

■ 解法
　始めに、カレンダーの法則（きまり）を見つけてみましょう。
まず目につくのは、縦に見た場合（曜日で見た場合）、７ずつ日が増えていることがわかると思います。例えば、火曜日を縦に見ると、１、８、１５・・・と７ずつ増えています。他の曜日も同様です。
　つまり、７日経つとまた同じ曜日に戻ってきます。言い換えるとカレンダーは７日を周期として成り立っているわけです。
曜日を求める問題はこの７日を一つのかたまりとして、割り算の余りをもとにして解くことができます。
ここで、見方を変えて、横に日にちを並べてみましょう。


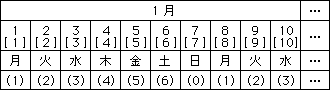
　（　）の中の数は、日にちを7で割ったときの余りです。この余りがカレンダーの問題を解くときのカギになります。この余りに注目してみると、次のようなもうひとつの法則がみつかります。
火曜日・・・日にちを７で割ったときの余りが１
水曜日・・・日にちを７で割ったときの余りが２
木曜日・・・日にちを７で割ったときの余りが３
金曜日・・・日にちを７で割ったときの余りが４
土曜日・・・日にちを７で割ったときの余りが５
日曜日・・・日にちを７で割ったときの余りが６
月曜日・・・日にちを７で割ったときの余りが０

■ 答え
（１）1月30日は、30÷7＝4　…2で余りが2だから、水曜日です。

（２）2月24日の曜日を求めるために、1月末から2月上旬を書き出してみましょう。
　右のカレンダーを見るとわかると思いますが、1月と2月とでは、日にちを7で割ったときの余りが曜日ごとに共通にならないので注意が必要です。
　つまり、7で割ったときの余りが1になるのは、火曜日ではなく、金曜日。余りが2になるのは、水曜日ではなく、土曜日なのです。
　よって、2月24日は、２４÷７＝３…３　で余りが３になるので、日曜日であることがわかります。

ただし、この方法で解いていくと、３ヵ月後、半年後の曜日を求めるためには、かなり苦戦しそうです。ところが、１つだけ工夫をすると、３ヶ月後でも、半年後でも、比較的簡単に曜日を求めることができます。次の表を見て下さい。２月１日を32、2月2日を33、2月3日を34・・・と考えるのです。すると、７で割ったときの余りが1月と同じになります。


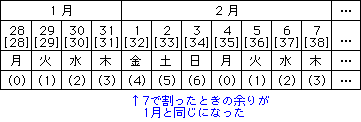
2月24日は1月から数えると、31＋24＝55になります。
7で割ると55÷7＝7…6　で余りが6になるので、日曜日であることがわかります。
このように工夫すれば、1月と同じ余りのルールで曜日を求めることができるのです。

以上がカレンダーの曜日についての問題を解くカギはすべて説明しました。それでは、次の問題に挑戦してみてください。

---

　2002年12月31日は火曜日です。2003年5月5日は何曜日でしょうか。ただし、2003年はうるう年ではないので、2003年2月は28日までです。

■ 解法
　まず、12月31日から1月上旬までのカレンダーを同様に書き出してみましょう。

　余りに着目すると、火曜日は1、水曜日は2、木曜日は3…であることがわかります。
　次に5月5日は12月31日から数えると、

１（12月）＋31（1月）＋28（２月）＋31（３月）＋30（４月）＋5（５月）＝126

曜日（余り）を求めるために7で割ると

126÷7＝18…0　
余りが0なので、2003年5月5日は月曜日であることがわかります。

■ 答え
月曜日

---

　2001年1月1日は月曜日でした。それでは、2005年の1月1日は何曜日になるでしょうか。ただし、2004年はうるう年なので、1年は366日になります。

■ 解法
今までと同様にカレンダーを書いてみましょう



365（2001年）＋365（2002年）＋365（2003年）＋366（2004年）＋1（2005年）＝1462

1462÷7＝208…6
余りが6なので、土曜日であることがわかります。

■ 答え
土曜日

■ うるう年について

西暦が４で割り切れる年が、うるう年で１年が３６６日となります。つまり、2000年、2004年、2008年・・・と4年ごとにうるう年がやってきます。ただし、1700年や1800年は4で割り切れる年ですが、100で割り切れ400で割り切れない年は閏年にはなりません。次は2100年が閏年の例外になります。詳しくは百科事典の「グレゴリオ暦」という項目を調べてみてください。 ちなみに4で割り切れる数は下2桁が4で割り切れれば（4の倍数であれば）、どんな数でも4で割り切れます。例えば、1012とか5914424などです。