食塩水の濃度

食塩水の濃度とは、ある食塩水を100ｇに相当させた場合、その中にどれくらいの食塩が溶けているかを表す数（割合）で、％（パーセント）で表します。この問題では、食塩30ｇと水170ｇを混ぜるから、できる上がる食塩水は200ｇです。この食塩水の中に含まれる食塩は30ｇです。

上図のように、食塩水200ｇ中に30ｇの食塩が含まれるということは、その半分の食塩水100ｇ相当では半分の食塩15ｇが含まれることなので15%です。

ウラワザ
　ここまでは濃度の意味を分かっていただくために理屈で説明しましたが、ここで、公式を２つ紹介します。次の２つの公式は少々複雑ですが、食塩の問題で登場させると簡単に解決してしまうのです。いわば、食塩問題ウルトラ２公式です。食塩濃度問題で困ったら、この2兄弟公式にHELPを求めると、かなり楽に解けますよ。

　ここで、この公式の説明と併せて、問題１をこの兄弟公式に頼って解いてみます。
問題１を解くために兄公式に登場してもらいます。（食塩）、（水）はそれぞれ食塩と水の量（ｇ）を表しています。（食塩）は30ｇ、（水）は170ｇですから、

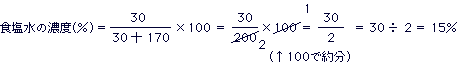
　弟公式に頼る場合は（食塩）を30ｇ、（食塩水）を200ｇとして（濃度）を求めます。ただし、弟公式は未熟なので、私たちのサポートも必要です。何が必要かというと、濃度が％で出ずに、0.15というような小数点で答えを出してきます。その小数を％に直してあげる必要があるのです。

答え：15％

　この問題も問題１と同じ考え方で解けます。食塩水の濃度とは、ある食塩水を100ｇに相当させた場合、その中にどれくらいの食塩が溶けているかを表す数（割合）です。濃度が10％の食塩水とは、食塩水100ｇ相当の中に食塩10ｇが溶けている食塩水です。つまり、水90ｇにつき10ｇの食塩を溶かすのです。

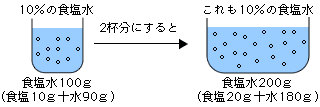
　いま、準備した食塩が20ｇあるので食塩水が200ｇできあがるように水を用意すれば、10％の食塩水ができますよね？つまり、180ｇの水を用意して、食塩20ｇを溶かして、200ｇの食塩水を作れば、10％の食塩水ができるわけです。つまり、必要な水の量は180ｇです。

ウラワザ
　問題2は、弟公式に頼って解いてみます。（食塩）が20ｇ、（濃度）を10％として、（食塩水）を求めます。ただし弟公式は％を小数にしないと対応できないので、10％は0.10（＝0.1）として与えます。

　　　　20＝（食塩水）×0.1　 (食塩水)に0.1をかけると20になるのだから、（食塩水）は200とすぐに分かる方は、以下の計算する必要はありません。

（食塩水）＝20÷0.1 ＝200ｇ

ここで、食塩水が200ｇと出ましたが、この問題では、水の量を出したいので、食塩の分20ｇを引いて、180ｇが答になります。

答え：180ｇ

まず、問題１と問題２の「ウラワザ」を見て、公式を理解してからこの解法を見てください。
「ウラワザ」でご紹介した、兄弟公式にフル活躍してもらってこの問題を解いてみましょう。

濃度を求めるので、兄公式が助けてくれそうです。「でも、、こんな問題どうやって公式にあてはめるの？」なんて思っていらっしゃる方も多いのでは・・・そこで、もう一度冷静に問題文をみてみましょう。分母はすぐわかるのではないでしょうか。兄公式の（食塩）＋（水）というのは、まさに（食塩水）の量のことですよね。ここでは、混ぜたあとの食塩水の濃度を求めることが目標です。混ぜたあとの食塩水の量は150ｇ＋100ｇで合計250ｇになります。これが分母。あとは、分子の（食塩）だけが分かれば、兄公式が一発解決してくれます。

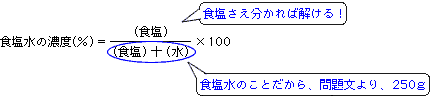
分子の食塩の量は弟公式が解決してくれます。すると次のように求めることができます。

この二つを混ぜれば、15ｇと5ｇで、合計20ｇの食塩が溶けている食塩水ができるはずです。だから、分子は20ｇ。あとは計算です。丁寧に計算してみましょう。

答え：8％