2004.04.13

方陣算

ご石やおはじきを正方形に並べるとき、1辺に並ぶ数、まわりに並ぶ数、全体の数などの間には一定の規則があります。この規則を利用して解く問題を方陣算といいます。今回はまず問題1で、その規則について説明します。問題2、問題3は応用問題です。方陣算を解くときの着眼点は正方形のいちばん外側の辺の個数です。このことを常に意識しながら読んでみてください。

問題1

ご石を1辺が5個の正方形になるように、すきまなく並べました。
（1）ご石の数は全部で何個ありますか。
（2）外側のまわりの数は何個ですか。
（3）たて、横を1列ずつふやすには、あと何個いりますか。
（4）外側のまわりに1列増やすにはあと何個いりますか。

解法

（1）
たてに5個、よこに5個だから　5×5＝25で合計25個です。

全体の数＝1辺の数×1辺の数

答え：25個

（2）
図のように、1辺の数より1個少ないかたまりを考えて4倍すれば、まわりの個数が計算できます。つまり、4×4＝16となり、16個が正解です。

まわりの数＝（1辺の数－1）×4

答え：16個

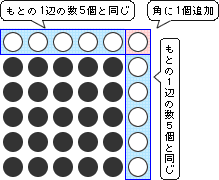
（3）
たて、横を1列ずつふやしたときの図は次の通りです。

たて・横を1列ふやすためには、
（もとの1辺の数の2倍）＋（角の1個）
のご石が必要となります。
･･･もとの1辺の個数の2倍よりも1個多く必要

たて、横を1列ずつふやすには、
2つ分と 1つ分が必要
つまり

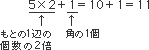
たて、横を1列ずつふやすには、あと11個必要となります。

答え：11個

（4）
外側のまわりに1列ふやした図は次の通りです。

外側のまわりに1列ふやすためには、
（もとの1辺の数の4倍）＋（角の4個）
が必要となります。
･･･もとの1辺の個数の4倍よりも4個多く必要

外側に1列増やすには、
が4つ分とが4つ分必要

もとの辺と同じ個数が4つ＋角の1個が4つ＝5×4＋1×4＝20＋4＝24個

答え：24個

問題1のまとめ（方陣算の規則）

	個数の計算方法
全体の個数	1辺の個数×1辺の個数
まわりの個数	(1辺の個数－1)×4
たて・横を1列ずつふやすとき	(もとの1辺の個数)×2＋1 ･･･もとの1辺の個数の2倍よりも1個多く必要
外側のまわりに1列ふやすとき	(もとの1辺の個数)×4＋4 ･･･もとの1辺の個数の4倍よりも4個多く必要

問題2

何個かのおはじきを正方形にならべたら20個あまりました。そこで、たても横も一列ずつ増やしたら15個足りなくなりました。おはじきは何個ありますか。

解法

問題文を図で表すと次のようになります。

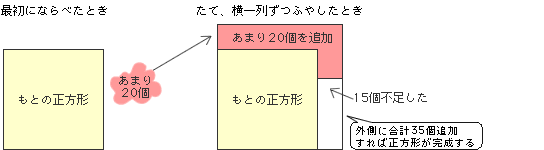
上の図より、外側に合計35個追加すれば、たて、横1列ずつ増やした正方形が完成することがわかります。
たて、横1列ずつ増やすためには、もとの正方形の1辺の個数の2倍より1個多くのおはじきが必要だから、この35個がもとの正方形の1辺の個数の2倍より1個多いだけの数と同じになります。
もとの正方形の1辺の個数は次のようにして考えます。

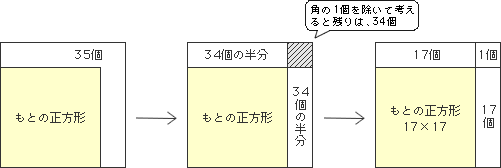
もとの正方形の1辺の個数は、35から1引いて半分にすれば計算できます。
つまり、

【もとの正方形をつくったおはじき個数】＝17×17＝289（個）

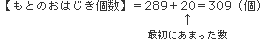
答え：309個

問題3

右の図のように、白と黒のご石を交互に使って、正方形をつくっていきます。いちばん外側の正方形の1辺にご石が14個ならんだとき、次の問いに答えなさい。
（1）白と黒のご石はそれぞれ何個ずつ使いましたか。
（2）いちばん外側のご石は何色で、何個になりますか。

解法

まず、色と1辺の個数の関係を内側から順に調べてみます。
図を見ると、色は白から始まり、外側に向かって交互に黒→白→黒→白･･･という順です。1辺の個数は内側から順に2個ずつ増えてゆきます。

色	白	黒	白	黒	白	黒	白
1辺の個数	2	4	6	8	10	12	14

次に正方形をつくるとき、それぞれ使ったご石の数を内側から順に計算します。
個数は（ひとつ内側の1辺の個数×4）＋4で計算できます。

色	白	黒	白	黒	白	黒	白
1辺の個数	2	4	6	8	10	12	14
使うご石の個数	4個	2×4＋4 ＝12個	4×4＋4 ＝20個	6×4＋4 ＝28個	8×4＋4 ＝36個	10×4＋4 ＝44個	12×4＋4 ＝52個

使った白のご石の数は、
4＋20＋36＋52＝112個

使った黒のご石の数は、
12＋28＋44＝84個

1辺の個数が14個だから、合計は
14×14＝196個
白は112個だから
黒は196－112＝84個と計算してもOKです。

いちばん外側のご石の数は、上の表より、52個。

1辺が14個だから
(14－1)×4＝13×4＝52
と計算してもOKです

（1）白112個、黒84個　（2)　白、52個

教え上手きんたろう先生

「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。

方陣算

問題1

解法

問題2

解法

問題3

解法

人気のテーマ

この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事

クリップした記事